The convolution integral: do some examples in Calculus III or not?

For us, calculus III is the most rushed of the courses, especially if we start with polar coordinates. Getting to the “three integral theorems” is a real chore. (ok, Green’s, Divergence and Stoke’s theorem is really just but that is the subject of another post)

But watching this lecture made me wonder: should I say a few words about how to calculate a convolution integral?

Note: I’ve discussed a type of convolution integral with regards to solving differential equations here.

In the context of Fourier Transforms, the convolution integral is defined as it was in analysis class: . Typically, we insist that the functions be, say, and note that it is a bit of a chore to show that the convolution of two functions is ; one proves this via the Fubini-Tonelli Theorem.

(The straight out product of two functions need not be ; e.g, consider for and zero elsewhere)

So, assuming that the integral exists, how do we calculate it? Easy, you say? Well, it can be, after practice.

But to test out your skills, let be the function that is for and zero elsewhere. So, what is ???

So, it is easy to see that only assumes the value of on a specific region of the plane and is zero elsewhere; this is just like doing an iterated integral of a two variable function; at least the first step. This is why it fits well into calculus III.

for the following region:

This region is the parallelogram with vertices at .

Now we see that we can’t do the integral in one step. So, the function we are integrating has the following description:

So the convolution integral is for and for .

That is, of course, the tent map that we described here. The graph is shown here:

So, it would appear to me that a good time to do a convolution exercise is right when we study iterated integrals; just tell the students that this is a case where one “stops before doing the outside integral”.

Nice collection of Math GIFs

No, these GIF won’t explain better than an instructor, but I found many of them to be fun.

Via: IFLS

How some mathematical definitions are made

I love what Brad Osgood says at 47:37.

The context: one is showing that the Fourier transform of the convolution of two functions is the product of the Fourier transforms (very similar to what happens in the Laplace transform); that is where

Fourier Transform of the “almost Gaussian” function with a residue integral

This is based on the lectures on the Fourier Transform by Brad Osgood from Stanford:

And here, provided the integral converges.

The “almost Gaussian” integrand is ; one can check that . One way is to use the fact that and do the substitution ; of course one should be able to demonstrate the fact to begin with. (side note: a non-standard way involving symmetries and volumes of revolution discovered by Alberto Delgado can be found here)

So, during this lecture, Osgood shows that ; that is, this modified Gaussian function is “its own Fourier transform”.

I’ll sketch out what he did in the lecture at the end of this post. But just for fun (and to make a point) I’ll give a method that uses an elementary residue integral.

Both methods start by using the definition:

Method 1: combine the exponential functions in the integrand:

. Now complete the square to get:

Now factor out the factor involving alone and write as a square:

Now, make the substitution to obtain:

Now we show that the above integral is really equal to

To show this, we perform along the retangular path : and let

Now the integral around the contour is 0 because is analytic.

We wish to calculate the negative of the integral along the top boundary of the contour. Integrating along the bottom gives 1.
As far as the sides: if we fix we note that and the magnitude goes to zero as So the integral along the vertical paths approaches zero, therefore the integrals along the top and bottom contours agree in the limit and the result follows.

Method 2: The method in the video
This uses “differentiation under the integral sign”, which we talk about here.

Stat with and note

Now we do integration by parts: and the integral becomes:

Now the first term is zero for all values of as . The second term is merely:

.

So we have shown that which is a differential equation in which has solution (a simple separation of variables calculation will verify this). Now to solve for the constant note that .

The result follows.

Now: which method was easier? The second required differential equations and differentiating under the integral sign; the first required an easy residue integral.

By the way: the video comes from an engineering class. Engineers need to know this stuff!

How to succeed at calculus, and why it is worth it!

This post is intended to help the student who is willing to put time and effort into succeeding in a college calculus class.

Part One: How to Study

The first thing to remember is that most students will have to study outside of class in order to learn the material. There are those who pick things up right away, but these students tend to be the rare exception.

Think of it this way: suppose you want to learn to play the piano. A teacher can help show you how to play it and provide a practice schedule. But you won’t be any good if you don’t practice.

Suppose you want to run a marathon. A coach can help you with running form, provide workout schedules and provide feedback. But if you don’t run those workouts, you won’t build up the necessary speed and endurance for success.

The same principle applies for college mathematics classes; you really learn the material when you study it and do the homework exercises.

Here are some specific tips on how to study:

1. It is optimal if you can spend a few minutes scanning the text for the upcoming lesson. If you do this, you’ll be alert for the new concepts as they are presented and the concepts might sink in quicker.

2. There is some research that indicates:
a. It is better to have several shorter study sessions rather than one long one and
b. There is an optimal time delay between study sessions and the associated lecture.

Look at it this way: if you wait too long after the lesson to study it, you would have forgotten much of what was presented. If you study right away, then you really have, in essence, a longer class room session. It is probably best to hit the material right when the initial memory starts to fade; this time interval will vary from individual to individual. For more on this and for more on learning for long term recall, see this article.

3. Learn the basic derivative formulas inside and out; that is, know what the derivatives of functions like are on sight; you shouldn’t have to think about them. The same goes for the basic trig identities such as and

Why is this? The reason is that much of calculus (though not all!) boils down to pattern recognition.

For example, suppose you need to calculate:

If you don’t know your differentiation formulas, this problem is all but impossible. On the other hand, if you do know your differentiation formulas, then you’ll immediately recognize the and it’s derivative and you’ll see that this problem is really the very easy problem .

But this all starts with having “automatic” knowledge of the derivative formulas.

Note: this learning is something your professor or TA cannot do for you!

4. Be sure to do some study problems with your notes and your book closed. If you keep flipping to your notes and book to do the homework problems, you won’t be ready for the exams. You have to kick up the training wheels.
Try this; the difference will surprise you. There is also evidence that forcing yourself to recall the material FROM YOUR OWN BRAIN helps you learn the material! Give yourself frequent quizzes on what you are learning.

5. When reviewing for an exam, study the problems in mixed fashion. For example, get some note cards and write problems from the various sections on them (say, some from 3.1, some from 3.2, some from 3.3, and so on), mix the cards, then try the problems. If you just review section by section, you’ll go into each problem knowing what technique to use each time right from the start. Many times, half of the battle is knowing which technique to use with each problem; that is part of the course! Do the problems in mixed order.

If you find yourself whining complaining “I don’t know where to start” it means that you don’t know the material well enough. Remember that a trained monkey can repeat specific actions; you have to be a bit better than that!

6. Read the book, S L O W L Y, with pen and paper nearby. Make sure that you work through the examples in the text and that you understand the reasons for each step.

7. For the “more theoretical” topics, know some specific examples for specific theorems. Here is what I am talking about:

a. Intermediate value theorem: recall that if , then but there is no such that . Why does this not violate the intermediate value theorem?

b. Mean value theorem: note also that there is no such that . Why does this NOT violate the Mean Value Theorem?

c. Series: it is useful to know basic series such as those for . It is also good to know some basic examples such as the geometric series, the divergent harmonic series and the conditionally convergent series .

d. Limit definition of derivative: be able to work a few basic examples of the derivative via the limit definition: and know why the derivative of and do not exist at .

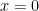Having some “template” example can help you master a theoretical concept.

Part II: Attitude
Your attitude will be very important.

1. Remember that your effort will be essential! Again, you can’t learn to run a marathon without getting off of the couch and making your muscles sore. Learning mathematics involves some frustration and, yes, at times, some tedium. Learning is fun OVERALL but it isn’t always fun at all times. You will encounter discomfort and unpleasantness at times.

2. Remember that winners look for ways to succeed; losers and whiners look for excuses for failure. You can always find those who will be willing to enable your underachievement. Instead, seek out those who bring out your best.

3. Success is NOT guaranteed; that is what makes success rewarding! Think of how good you’ll feel about yourself if you mastered something that seemed impossible to master at first. And yes, anyone who has achieved anything that is remotely difficult has taken some lumps and bruises along the way. You will NOT be spared these.

Remember that if you duck the calculus challenge, you are, in essence, slamming many doors of opportunity shut right from the get-go.

4. On the other hand, remember that Calculus (the first two semesters anyway) is a Freshman level class; exceptional mathematical talent is not a prerequisite for success. True, calculus is easy for some but that isn’t the point. Most reasonably intelligent people can have success, if they are willing to put forth the proper effort in the proper manner.

Just think of how good it will feel to succeed in an area that isn’t your strong suit!

Dinette set on calculus…

Note: if you haven’t followed Julie Larson’s comic strip Dinette Set, the characters featured in it are not, well, the world’s most intellectually minded characters (with the exception of Patty). 🙂

Ironically, I see such attitudes displayed by people…posting their thoughts on the internet via a computer or smart phone. The irony doesn’t even occur to them.

Fields Medal 2014 and Mathfest 2011

One of the main speakers at Mathfest, 2011, was one of the Fields Medalists this year: Manjur Bhargava, of Princeton.

Here is what I said about him on the first day:

Lastly Manjul Bhargava of Princeton (who is already full professor though he is less than half my age; he was an Andrew Wiles student) gave a delightful lecture on algebraic curves.

What I noted: all three of these mathematicians are successful enough to be arrogant (especially the third). They could have blown us all away. Yes, they took the time and care to give presentations that actually taught us something.

Some top-of-the-line researchers are excellent teachers too.

Almost ready to start the semester again…

I am teaching two freshman sections…it is a breaking in process for them.

Calculation of the Fourier Transform of a tent map, with a calculus tip….

I’ve been following these excellent lectures by Professor Brad Osgood of Stanford. As an aside: yes, he is dynamite in the classroom, but there is probably a reason that Stanford is featuring him. 🙂

And yes, his style is good for obtaining a feeling of comradery that is absent in my classroom; at least in the lower division “service” classes.

This lecture takes us from Fourier Series to Fourier Transforms. Of course, he admits that the transition here is really a heuristic trick with symbolism; it isn’t a bad way to initiate an intuitive feel for the subject though.

However, the point of this post is to offer a “algebra of calculus trick” for dealing with the sort of calculations that one might encounter.

By the way, if you say “hey, just use a calculator” you will be BANNED from this blog!!!! (just kidding…sort of. 🙂 )

So here is the deal: let represent the tent map: the support of is and it has the following graph:

The formula is:

So, the Fourier Transform is

Now, this is an easy integral to do, conceptually, but there is the issue of carrying constants around and being tempted to make “on the fly” simplifications along the way, thereby leading to irritating algebraic errors.

So my tip: just let and do the integrals:

and substitute and simplify later:

Now the integrals become:
These are easy to do; the first is merely and the next two have the same anti-derivative which can be obtained by a “integration by parts” calculation: ; evaluating the limits yields:

Add the first integral and simplify and we get: . NOW use and we have the integral is by Euler’s formula.

Now we need some trig to get this into a form that is “engineering/scientist” friendly; here we turn to the formula: so so our answer is which is often denoted as as the “normalized” function is given by (as we want the function to have zeros at integers and to “equal” one at (remember that famous limit!)

So, the point is that using made the algebra a whole lot easier.

Now, if you are shaking your head and muttering about how this calculation was crude that that one usually uses “convolution” instead: this post is probably too elementary for you. 🙂

Interchanging infinite sums with integrals

This part of this series of lectures got me to thinking about this topic; the relevant part starts at 13 minutes:

(side note: I am enjoying these and hope to finish all 30!)

Of interest here: if describes the heat in a one dimensional circle of metal and the radius is one, one can do the analysis of the heat equation with initial condition and assuming that has a Fourier expansion (complex coefficients) one can obtain: which can be rewritten as . Note: ranges from to and by we mean and note that are complex conjugates for all .

Now IF we could interchange the summation sign and the integral sign we’d have: . Now let then we could say that which is a convolution product; is the heat kernel which is a nice form. But about that interchange: when can we do it?

First note that by we mean the limit of the sequence of partial sums: and if then the interchange is valid. NOTE: I am following the custom of not using the “differential” and of letting it be understood that means .

The “I don’t want “TL;DR” answer” version
If you are comfortable with Lebesgue integration, then the Dominated Convergence Theorem is the standard: if are all measurable functions and (pointwise) and there exists an integrable function where for all , then .

Now if the terms “Lebesgue integration” and “measurable” has you scratching your head, you can either learn a bit about it or, if you are in the “tl;dr” mode I’ll make some (hopefully) “practitioner friendly” remarks.

First of all, all Riemann integrable functions are Lebesgue integrable (provided we are NOT talking about improper integrals) and a “measurable function” is one in which the inverse image of a “measurable set” is a “measurable set”. Now “measurable set”: these include sets that single point sets, open intervals, closed intervals, countable intersections of such, countable unions of such and complements of such unions and intersections. Unfortunately there are measurable sets that aren’t formed in this manner, and there are such things as non-measurable sets. See here for the definition of “measurable set”.

Upshot: the sort of functions that appear in Fourier Series are measurable so you probably don’t have to worry. So there is probably no harm in assuming that the are Riemann integrable functions.

Pointwise convergence: this means for all in the domain of interest (here, ), .

Of course, when we are talking about the Fourier series for a given function , there are conditions that must be met to get that the the series converges to a function that is “almost “; the video assumes that is which means that exists. The mathematics of convergence of a Fourier series is rich; for this note we will assume that the Fourier series in question converges.

Now for the conclusion: assuming that the converge pointwise to some then but we need to use the Lebesgue integral to guarantee this equality..in general. This is why:

For example, suppose we enumerate the rational numbers by and define and then inductively define . Then and for each , but , the limit function, is not Riemann integrable. It is Lebesgue integrable though, and the integral remains 1.

But, given the types of series that the practitioner will be working with (typically: only a finite number of maximums and minimums on a given interval and a finite number of jump discontinuities), one will probably not encounter such pathological behavior with the functions. I give this example to explain why the Dominated Convergence Theorem uses Lebesgue integrals.

Wait a minute you might say, didn’t I read something about “uniform convergence” of functions that lead to the limiting behavior that we need? Well, yes, and I’ll explain that here:

we say that uniformly if for any there exists such that for all , for ALL in the interval of interest. Then, it a routine exercise in Riemann integration to see that if uniformly then . The down side is that we rarely have uniform convergence when we are talking about Fourier series terms. Here is why: it is known that if uniformly and that if all of the are continuous, then the limit function is continuous as well. However when one obtains the Fourier series for a function with jump discontinuities (say, for a pulse wave) one sees that the terms (and hence the sequence of partial sums) of the Fourier series are continuous but what the Fourier series converges to is not continuous; hence the convergence of the series is NOT uniform.