College Math Teaching

July 14, 2020

An alternative to trig substitution, sort of..

Filed under: calculus, change of variable, derivatives, integrals, integration by substitution — Tags: — oldgote @ 1:52 am

Ok, just for fun: \int \sqrt{1+x^2} dx =

The usual is to use x =tan(t), dx =sec^2(t) dt which transforms this to the dreaded \int sec^3(t) dt integral, which is a double integration by parts.
Is there a way out? I think so, though the price one pays is a trickier conversion back to x.

Let’s try x =sinh(t) \rightarrow dx = cosh(t) dt so upon substituting we obtain \int |cosh(t)|cosh(t) dt and noting that cosh(t) > 0 alaways:

\int cosh^2(t)dt Now this can be integrated by parts: let u=cosh(t) dv = cosh(t) dt \rightarrow du =sinh(t), v = sinh(t)

So \int cosh^2(t)dt = cosh(t)sinh(t) -\int sinh^2(t)dt but this easily reduces to:

\int cosh^2(t)dt = cosh(t)sinh(t) -\int cosh^2(t)-1 dt \rightarrow 2\int cosh^2(t)dt = cosh(t)sinh(t) -t + C

Division by 2: \int cosh^2(t)dt = \frac{1}{2}(cosh(t)sinh(t)-t)+C

That was easy enough.

But we now have the conversion to x: \frac{1}{2}(cosh(t)sinh(t) \rightarrow \frac{1}{2}x \sqrt{1+x^2}

So far, so good. But what about t \rightarrow arcsinh(x) ?

Write: sinh(t) = \frac{e^{t}-e^{-t}}{2} = x \rightarrow e^{t}-e^{-t} =2x \rightarrow e^{t}-2x -e^{-t} =0

Now multiply both sides by e^{t} to get e^{2t}-2xe^t -1 =0 and use the quadratic formula to get e^t = \frac{1}{2}(2x\pm \sqrt{4x^2+4} \rightarrow e^t = x \pm \sqrt{x^2+1}

We need e^t > 0 so e^t = x + \sqrt{x^2+1} \rightarrow t = ln|x + \sqrt{x^2+1}| and that is our integral:

\int \sqrt{1+x^2} dx = \frac{1}{2}x \sqrt{1+x^2} + \frac{1}{2} ln|x + \sqrt{x^2+1}| + C

I guess that this isn’t that much easier after all.

July 12, 2020

Logarithmic differentiation: do we not care about domains anymore?

Filed under: calculus, derivatives, elementary mathematics, pedagogy — collegemathteaching @ 11:29 pm

The introduction is for a student who might not have seen logarithmic differentiation before: (and yes, this technique is extensively used..for example it is used in the “maximum likelihood function” calculation frequently encountered in statistics)

Suppose you are given, say, f(x) =sin(x)e^x(x-2)^3(x+1) and you are told to calculate the derivative?

Calculus texts often offer the technique of logarithmic differentiation: write ln(f(x)) = ln(sin(x)e^x(x-2)^3(x+1)) = ln(sin(x)) + x + 3ln(x-2) + ln(x+1)
Now differentiate both sides: ln((f(x))' = \frac{f'(x)}{f(x)} = \frac{cos(x)}{sin(x)} + 1 + \frac{3}{x-2} + {1 \over x+1}

Now multiply both sides by 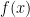f(x) to obtain

f'(x) = f(x)(\frac{cos(x)}{sin(x)} + 1 + \frac{3}{x-2} + {1 \over x+1}) =

\

(sin(x)e^x(x-2)^3(x+1)(\frac{cos(x)}{sin(x)} + 1 + \frac{3}{x-2} + {1 \over x+1})

And this is correct…sort of. Why I say sort of: what happens, at say, 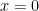x = 0 ? The derivative certainly exists there but what about that second factor? Yes, the sin(x) gets cancelled out by the first factor, but AS WRITTEN, there is an oh-so-subtle problem with domains.

You can only substitute x \in \{ 0, \pm k \pi \} only after simplifying ..which one might see as a limit process.

But let’s stop and take a closer look at the whole process: we started with f(x) = g_1(x) g_2(x) ...g_n(x) and then took the log of both sides. Where is the log defined? And when does ln(ab) = ln(a) + ln(b) ? You got it: this only works when a > 0, b > 0 .

So, on the face of it, ln(g_1 (x) g_2(x) ...g_n(x)) = ln(g_1(x) ) + ln(g_2(x) ) + ...ln(g_n(x)) is justified only when each g_i(x) > 0 .

Why can we get away with ignoring all of this, at least in this case?

Well, here is why:

1. If f(x) \neq 0 is a differentiable function then \frac{d}{dx} ln(|f(x)|) = \frac{f'(x)}{f(x)}
Yes, this is covered in the derivation of \int {dx \over x} material but here goes: write

|f(x)| = \begin{cases} f(x) ,& \text{if } f(x) > 0 \\ -f(x), & \text{otherwise} \end{cases}

Now if f(x) > 0 we get { d \over dx} ln(f(x)) = {f'(x) \over f(x) } as usual. If f(x) < 0 then |f(x)| = =f(x), |f(x)|' = (-f(x))' = -f'(x) and so in either case:

\frac{d}{dx} ln(|f(x)|) = \frac{f'(x)}{f(x)} as required.

THAT is the workaround for calculating {d \over dx } ln(g_1(x)g_2(x)..g_n(x)) where g_1(x)g_2(x)..g_n(x) \neq 0 : just calculate {d \over dx } ln(|g_1(x)g_2(x)..g_n(x)|) . noting that |g_1(x)g_2(x)..g_n(x)| = |g_1(x)| |g_2(x)|...|g_n(x)|

Yay! We are almost done! But, what about the cases where at least some of the factors are zero at, say x= x_0 ?

Here, we have to bite the bullet and admit that we cannot take the log of the product where any of the factors have a zero, at that point. But this is what we can prove:

Given g_1(x) g_2(x)...g_n(x) is a product of differentiable functions and g_1(a) g_2(a)...g_k(a) = 0 k \leq n then
(g_1(a)g_2(a)...g_n(a))' = lim_{x \rightarrow a} g_1(x)g_2(x)..g_n(x) ({g_1'(x) \over g_1(x)} + {g_2'(x) \over g_2(x)} + ...{g_n'(x) \over g_n(x})

This works out to what we want by cancellation of factors.

Here is one way to proceed with the proof:

1. Suppose 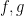f, g are differentiable and f(a) = g(a) = 0 . Then (fg)'(a) = f'(a)g(a) + f(a)g'(a) = 0 and lim_{x \rightarrow a} f(x)g(x)({f'(x) \over f(x)} + {g'(x) \over g(x)}) = 0
2. Now suppose 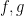f, g are differentiable and f(a) =0 , g(a) \neq 0 . Then (fg)'(a) = f'(a)g(a) + f(a)g'(a) = f'(a)g(a) and lim_{x \rightarrow a} f(x)g(x)({f'(x) \over f(x)} + {g'(x) \over g(x)}) = f'(a)g(a)
3.Now apply the above to g_1(x) g_2(x)...g_n(x) is a product of differentiable functions and g_1(a) g_2(a)...g_k(a) = 0 k \leq n
If k = n then (g_1(a)g_2(a)...g_n(a))' = lim_{x \rightarrow a} g_1(x)g_2(x)..g_n(x) ({g_1'(x) \over g_1(x)} + {g_2'(x) \over g_2(x)} + ...{g_n'(x) \over g_n(x}) =0 by inductive application of 1.

If 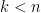k < n then let g_1...g_k = f, g_{k+1} ..g_n =g as in 2. Then by 2, we have (fg)' = f'(a)g(a) Now this quantity is zero unless k = 1 and f'(a) neq 0 . But in this case note that lim_{x \rightarrow a} g_1(x)g_2(x)...g_n(x)({g_1'(x) \over g_1(x)} + {g_2'(x) \over g_2(x)} + ...+ {g_n'(x) \over g_n(x)}) = lim_{x \rightarrow a} g_2(x)...g_n(x)(g_1'(x)) =g(a)g_1(a)

So there it is. Yes, it works ..with appropriate precautions.

July 10, 2020

This always bothered me about partial fractions…

Filed under: algebra, calculus, complex variables, elementary mathematics, integration by substitution — Tags: — collegemathteaching @ 12:03 am

Let’s look at an “easy” starting example: write \frac{1}{(x-1)(x+1)} = \frac{A}{x-1} + \frac{B}{x+1}
We know how that goes: multiply both sides by (x-1)(x+1) to get 1 = A(x+1) + B(x-1) and then since this must be true for ALL x , substitute x=-1 to get B = -{1 \over 2} and then substitute x = 1 to get A = {1 \over 2} . Easy-peasy.

BUT…why CAN you do such a substitution since the original domain excludes x =1, x = -1 ?? (and no, I don’t want to hear about residues and “poles of order 1”; this is calculus 2. )

Lets start with \frac{1}{(x-1)(x+1)} = \frac{A}{x-1} + \frac{B}{x+1} with the restricted domain, say x \neq 1
Now multiply both sides by x-1 and note that, with the restricted domain x \neq 1 we have:

\frac{1}{x+1} = A + \frac{B(x-1)}{x+1} But both sides are equal on the domain (-1, 1) \cup (1, \infty) and the limit on the left hand side is lim_{x \rightarrow 1} {1 \over x+1 } = {1 \over 2} So the right hand side has a limit which exists and is equal to A . So the result follows..and this works for the calculation for B as well.

Yes, no engineer will care about this. But THIS is the reason we can substitute the non-domain points.

As an aside: if you are trying to solve something like {x^2 + 3x + 2 \over (x^2+1)(x-3) } = {Ax + B \over x^2+1 } + {C \over x-3 } one can do the denominator clearing, and, as appropriate substitute x = i and compare real and imaginary parts ..and yes, now you can use poles and residues.

July 3, 2020

What will happen this fall?

Filed under: COVID19, pedagogy — Tags: — collegemathteaching @ 12:22 am

Yes, I should be doing math but, well, I can tell you what I’ve done since online and many of my summer duties have ended:

1. I’ve purchased some “stuff for hybrid learning” equipment, to wit: drawing board and a document camera.
2. I also have a gallon of hand sanitizer, face shield and 100 masks to hand out to students who “forget” to wear one to class.

Yes, I know, my university announced that we will start in person, go to Thanksgiving and then finish remotely. And exactly how far we get remains to be seen; I know that USC just announced that they are going online from the start.

That might get the dominoes falling.

But here are my plans for my two “hybrid” classes (4 meetings a week, but due to social distance limits, half the class will come M, Th, half on W, F)
a. Stuff in the lessons is mandatory; students are responsible for notes, quizzes, assignments
b. But, I will NOT require in person attendance, ever. All notes will be posted on line (I am working on them right now), all class room sessions will be put on video (maybe even live streamed) and
c. All testing, quizzes, etc. will be online. Yes, they will be open book; that is really the only way to be fair. Hence I’ll have to be creative with my exams.

As far as my actuarial science class: similar, though this class should be able to meet social distancing requirements. My not requiring in person attendance is for the students (e. g. what if they are worried, have some sort of medical condition, etc.)

I did attend a two week session on online learning and have some ideas on how to upload videos and the like. I’ll do some experimenting beforehand.

And yes, I have two papers to finish; I hope that this note gets me inspired to get back to it.

Create a free website or blog at WordPress.com.