Ok, a mathematician who is known to be brilliant self-publishes (on the internet) a dense, 512 page proof of a famous conjecture. So what happens?
The Internet exploded. Within days, even the mainstream media had picked up on the story. “World’s Most Complex Mathematical Theory Cracked,” announced the Telegraph. “Possible Breakthrough in ABC Conjecture,” reported the New York Times, more demurely.
On MathOverflow, an online math forum, mathematicians around the world began to debate and discuss Mochizuki’s claim. The question which quickly bubbled to the top of the forum, encouraged by the community’s “upvotes,” was simple: “Can someone briefly explain the philosophy behind his work and comment on why it might be expected to shed light on questions like the ABC conjecture?” asked Andy Putman, assistant professor at Rice University. Or, in plainer words: I don’t get it. Does anyone?
The problem, as many mathematicians were discovering when they flocked to Mochizuki’s website, was that the proof was impossible to read. The first paper, entitled “Inter-universal Teichmuller Theory I: Construction of Hodge Theaters,” starts out by stating that the goal is “to establish an arithmetic version of Teichmuller theory for number fields equipped with an elliptic curve…by applying the theory of semi-graphs of anabelioids, Frobenioids, the etale theta function, and log-shells.”
This is not just gibberish to the average layman. It was gibberish to the math community as well.
[…]
Here is the deal: reading a mid level mathematics research paper is hard work. Refereeing it is even harder work (really checking the proofs) and it is hard work that is not really going to result in anything positive for the person doing the work.
Of course, if you referee for a journal, you do your best because you want YOUR papers to get good refereeing. You want them fairly evaluated and if there is a mistake in your work, it is much better for the referee to catch it than to look like an idiot in front of your community.
But this work was not submitted to a journal. Interesting, no?
Of course, were I to do this, it would be ok to dismiss me as a crank since I haven’t given the mathematical community any reason to grant me the benefit of the doubt.
And speaking of idiots; I made a rather foolish remark in the comments section of this article by Edward Frenkel in Scientific American. The article itself is fine: it is about the Abel prize and the work by Pierre Deligne which won this prize. The work deals with what one might call the geometry of number theory. The idea: if one wants to look for solutions to an equation, say,  one gets different associated geometric objects which depend on “what kind of numbers” we allow for
one gets different associated geometric objects which depend on “what kind of numbers” we allow for  . For example, if
. For example, if 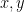 are integers, we get a 4 point set. If
are integers, we get a 4 point set. If  are real numbers, we get a circle in the plane. Then Frenkel remarked:
are real numbers, we get a circle in the plane. Then Frenkel remarked:
such as x2 + y2 = 1, we can look for its solutions in different domains: in the familiar numerical systems, such as real or complex numbers, or in less familiar ones, like natural numbers modulo N. For example, solutions of the above equation in real numbers form a circle, but solutions in complex numbers form a sphere.
The comment that I bolded didn’t make sense to me; I did a quick look up and reviewed that  actually forms a 3-sphere which lives in
actually forms a 3-sphere which lives in  . Note: I added in the “absolute value” signs which were not there in the article.
. Note: I added in the “absolute value” signs which were not there in the article.
This is easy to see: if  then
then  implies that
implies that  . But that isn’t what was in the article.
. But that isn’t what was in the article.
Frenkel made a patient, kind response …and as soon as I read “equate real and imaginary parts” I winced with self-embarrassment.
Of course, he admits that the complex version of this equation really yields a PUNCTURED sphere; basically a copy of 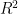 in
in  .
.
Just for fun, let’s look at this beast.
Real part of the equation: 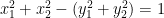
Imaginary part:  (for you experts: this is a real algebraic variety in 4-space).
(for you experts: this is a real algebraic variety in 4-space).
Now let’s look at the intersection of this surface in 4 space with some coordinate planes:
Clearly this surface misses the  plane (look at the real part of the equation).
plane (look at the real part of the equation).
Intersection with the  plane yields
plane yields  which is just the unit circle.
which is just the unit circle.
Intersection with the  plane yields the hyperbola
plane yields the hyperbola 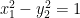
Intersection with the  plane yields the hyperbola
plane yields the hyperbola 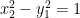
Intersection with the  plane yields two isolated points:
plane yields two isolated points: 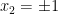
Intersection with the  plane yields two isolated points:
plane yields two isolated points: 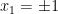
(so we know that this object is non-compact; this is one reason the “sphere” remark puzzled me)
Science and the media
This Guardian article points out that it is hard to do good science reporting that goes beyond information entertainment. Of course, one of the reasons is that many “groundbreaking” science findings turn out to be false, even if the scientists in question did their work carefully. If this sounds strange, consider the following “thought experiment”: suppose that there are, say, 1000 factors that one can study and only 1 of them is relevant to the issue at hand (say, one place on the genome might indicate a genuine risk factor for a given disease, and it makes sense to study 1000 different places). So you take one at random, run a statistical test at  and find statistical significance at
and find statistical significance at  . So, if we get a “positive” result from an experiment, what is the chance that it is a true positive? (assume 95 percent accuracy)
. So, if we get a “positive” result from an experiment, what is the chance that it is a true positive? (assume 95 percent accuracy)
So let P represent a positive outcome of a test, N a negative outcome, T means that this is a genuine factor, and F that it isn’t.
Note: P(T) = .001, P(F) = .999,  . It follows
. It follows 
So we seek: the probability that a result is true given that a positive test occurred: we seek  . That is, given a test is 95 percent accurate, if one is testing for something very rare, there is only about a 2 percent chance that a positive test is from a true factor, even if the test is done correctly!
. That is, given a test is 95 percent accurate, if one is testing for something very rare, there is only about a 2 percent chance that a positive test is from a true factor, even if the test is done correctly!
; examples might be:
. I’ll denote these series by
.
of “bounded power” if there exists some integer
such that
for all
; that is,
for some
.
will be called equivalent if there exists an integer (possibly negative or zero)
such that
. The multiplication here is understood to be formal “term by term” multiplication.
be a sequence of equivalent Laurent series. We say that the sequence
converges to a Laurent series
if for every positive integer
we can find an integer
such that for all
,
; that is, the difference is a non-Laurent series whose smallest power becomes arbitrarily large as the sequence of Laurent series gets large.
converges to
.
