Workshop in Geometric Topology: TCU 2015 morning session 1

I’ll be blunt: I’ve been teaching at a 11-12 hour load (mostly 11; one time I had a 9 hour load; 3 courses) since fall, 1991. Though I’ve published, most of what I’ve done has been extremely “bare handed”; it is tough to learn the most advanced techniques (which is a full time job in and of itself)

So, at math conferences, I get to see how much further behind I’ve fallen.

But these things help in the following way:

1. They are an excellent change of pace from the usual routine of teaching calculus.
2. I do learn things, even if it is “looking up” a definition or two; for example I looked up the definition of “pure braid group” in between the 20 minute talks.
3. I have to review my own stuff to see if I am indeed making progress; I don’t want to say something idiotic in front of some very smart, informed people.

But yes, the talks have been given by smart, (mostly) young, energetic people who have been studying the topic that they are talking about very intensely for a long time; frequently it is tough to hang in to the second half of the 20 minute talks. But I can see WHAT is being studied, what tools are being used and, as I said before, find stuff to look up.

The final talk: didn’t understand much beyond the general gist but it was well organized, well presented..exactly what you get when you have a brilliant energetic young researcher working full time in mathematical research.

On one hand, I envy his talent. On the other hand, I am glad that we have some smart humans among us; they benefit all of us.

The trip here The plane was about 2.5 hours late getting in, then there was a long ride to the car rental place and a 35 minute drive to campus, then finding my way around in the dark. So no morning run; I might do a gentle “after the talks” focused walk (5K-ish?).

I talk at 9 am tomorrow and I want to make it worth their while.

Unsolicited advise to young professors at heavy teaching load universities: Go to Research Conferences anyway!

This is coming to you from Ames, Iowa at the Spring American Mathematical Society Meeting. I am here to attend the sessions on the Topology of 3-dimensional manifolds.

Note: I try to go to conferences regularly; I have averaged about 1 conference a year. Sometimes, the conference is a MAA Mathfest conference. These ARE fun and refreshing. But sometimes (this year), I go to a research oriented conference.

I’ll speak for myself only.

Sometimes, these can be intimidating. Though many of the attendees are nice, cordial and polite, the fact is that many (ok, almost all of them) are either the best graduate students or among the finest researchers in the world. The big names who have proved the big theorems are here. They earn their living by doing cutting edge research and by guiding graduate students through their research; they are not spending hours and hours convincing students that .

So, the talks can be tough. Sure, they do a good job, but remember that most of the audience is immersed in this stuff; they don’t have to review things like “normal surface theory” or “Haken manifold”.

Therefore, it is VERY easy to start lamenting (internally) “oh no, I am by far the dumbest one here”. That, in my case, IS true, but it is unimportant.
What I found is that, if I pay attention to what I can absorb, I can pick up a technique here and there, which I can then later use in my own research. In fact, just today, I picked up something that might help me with a problem that I am pondering.

Also, the atmosphere can be invigorating!

I happen to enjoy the conferences that are held on university campuses. There is nothing that gets my intellectual mood pumped up more than to hang around the campus of a division I research university. For me, there is nothing like it.

This conference
A few general remarks:
1. I didn’t realize how pretty Iowa State University is. I’d rank it along with the University of Tennessee as among the prettiest campuses that I’ve ever seen.

2. As far as the talks: one “big picture” technique that I’ve seen used again and again is the technique of: take an abstract set of objects (say, the Seifert Surfaces of a knot; say of minimal genus. Then to each, say, ambient isotopy class of Seifert Surface, assign a vertex of a graph or simplicial complex. Then group the vertices together either by a segment (in some settings) or a simplex (if, in one setting, the Seifert Surfaces admit disjoint representatives). Then one studies the complex or the graph.

In one of the talks (talking about essential closed surfaces in the complement of a knot), one assigned such things to the vertex of a graph (dendron actually) and set up an algorithm to search along such a graph; it turns out that is one starts near the top of this dendron, one gains the opportunity to prune lower branches of the group by doing the calculation near the top.

Sidenote
The weather couldn’t be better; I found time over lunch to do a 5.7 mile run near my hotel. The run was almost all on bike paths (albeit a “harder” surface than I’d like).

Day 2, Madison MAA Mathfest

The day started with a talk by Karen King from the National Council of Teachers of Mathematics.
I usually find math education talks to be dreadful, but this one was pretty good.

The talk was about the importance of future math teachers (K-12) actually having some math background. However, she pointed out that students just having passed math courses didn’t imply that they understood the mathematical issues that they would be teaching…and it didn’t imply that their students would do better.

She gave an example: about half of those seeking to teach high school math couldn’t explain why “division by zero” was undefined! They knew that it was undefined but couldn’t explain why. I found that astonishing since I knew that in high school.

Later, she pointed out that potential teachers with a math degree didn’t understand what the issues were in defining a number like . Of course, a proper definition of this concept requires at least limits or at least a rigorous definition of the log function and she was well aware that the vast majority of high school students aren’t ready for such things. Still, the instructor should be; as she said “we all wave our hands from time to time, but WE should know when we are waving our hands.”

She stressed that we need to get future math teachers to get into the habit (she stressed the word: “habit”) of always asking themselves “why is this true” or “why is it defined in this manner”; too many of our math major courses are rule bound, and at times we write our exams in ways that reward memorization only.

Next, Bernd Sturmfels gave the second talk in his series; this was called Convex Algebraic Geometry.

You can see some of the material here. He also lead this into the concept of “Semidefinite programming”.

The best I can tell: one looks at the objects studied by algebraic geometers (root sets of polynomials of several variables) and then takes a “affine slice” of these objects.

One example: the “n-ellipse” is the set of points on the plane that satisfy where are points in the plane.

Questions: what is the degree of the polynomial that describes the ellipse? What happens if we let tend to zero? What is the smallest for which the ellipse is non-vanishing (Fermat-Webber point)? Note: the 2 ellipse is the circle, the 3 ellipse (degree 8) is what we usually think of as an ellipse.

Note: these type of surfaces can be realized as the determinant of a symmetric matrix; these matrices have real eigenvalues. We can plot curves over which an eigenvalue goes to zero and then changes sign. This process leads to what is known as a spectrahedron ; this is a type of shape in space. A polyhedron can be thought of as the spectrahedron of a diagonal matrix.

Then one can seek to optimize a linear function over a spectrahedron; this leads to semidefinite programming, which, in general, is roughly as difficult as linear programming.

One use: some global optimization problems can be reduced to a semidefinite programming problem (not all).

Shorter Talks
There was a talk by Bob Palais which discussed the role of Rodrigues in the discovery of the quaternions. The idea is that Rodrigues discovered the quaternions before Hamilton did; but he talked about these in terms of rotations in space.

There were a few talks about geometry and how to introduce concepts to students; of particular interest was the concept of a geodesic. Ruth Berger talked about the “fish swimming in jello” model: basically suppose you had a sea of jello where the jello’s density was determined by its depth with the most dense jello (turning to infinite density) at the bottom; and it took less energy for the fish to swim in the less dense regions. Then if a fish wanted to swim between two points, what path would it take? The geometry induced by these geodesics results in the upper half plane model for hyperbolic space.

Nick Scoville gave a talk about discrete Morse theory. Here is a user’s guide. The idea: take a simplicial complex and assign numbers (integers) to the points, segments, triangles, etc. The assignment has to follow rules; basically the boundary of a complex has to have a lower number that what it bounds (with one exception….) and such an assignment leads to a Morse function. Critical sets can be defined and the various Betti numbers can be calculated.

Christopher Frayer then talked about the geometry of cubic polynomials. This is more interesting than it sounds.
Think about this: remember Rolles Theorem from calculus? There is an analogue of this in complex variables called the Guass-Lucas Theorem. Basically, the roots of the derivative lie in the convex hull of the roots of the polynomial. Then there is Marden’s Theorem for polynomials of degree 3. One can talk about polynomials that have a root of and two other roots in the unit circle; then one can study where the the roots of the derivative lie. For a certain class of these polynomials, there is a dead circle tangent to the unit circle at 1 which encloses no roots of the derivative.

MAA Mathfest Madison Day 1, 2 August 2012

I am sitting in the main ballroom waiting for the large public talks to start. I should be busy most of the day; it looks as if there will be some interesting all day long.

I like this conference not only for the variety but also for the timing; it gives me some momentum going into the academic year.

I regret not taking my camera; downtown Madison is scenic and we are close to the water. The conference venue is just a short walk away from the hotel; I see some possibilities for tomorrow’s run. Today: just weights and maybe a bit of treadmill in the afternoon.

The Talks
The opening lecture was the MAA-AMS joint talk by David Mumford of Brown University. This guy’s credentials are beyond stellar: Fields Medal, member of the National Academy of Science, etc.

His talk was about applied and pure mathematics and how there really shouldn’t be that much of a separation between the two, though there is. For one thing: pure mathematics prestige is measured by the depth of the result; applied mathematical prestige is mostly measured by the utility of the produced model. Pure mathematicians tend to see applied mathematics as shallow and simple and they resent the fact that applied math…gets a lot more funding.

He talked a bit about education and how the educational establishment ought to solicit input from pure areas; he also talked about computer science education (in secondary schools) and mentioned that there should be more emphasis on coding (I agree).

He mentioned that he tended to learn better when he had a concrete example to start from (I am the same way).

What amused me: his FIRST example was on PDE (partial differential equations) model of neutron flux through nuclear reactors used for submarines; note that these reactors were light water, thermal reactors (in that the fission reaction became self sustaining via the absorption of neutrons whose energy levels had been lowered by a moderator (the neutrons lose energy when they collide with atoms that aren’t too much heavier).

Of course, in nuclear power school, we studied the PDEs of the situation after the design had been developed; these people had to come up with an optimal geometry to begin with.

Note that they didn’t have modern digital computers; they used analogue computers modeled after simple voltage drops across resistors!

About the PDE: you had two neutron populations: “fast” neutrons (ones at high energy levels) and “slow” neutrons (ones at lower energy levels). The fast neutrons are slowed down to become thermal neutrons. But thermal neutrons in turn cause more fissions thereby increasing the fast neutron flux; hence you have two linked PDEs. Of course there is leakage, absorption by control rods, etc., and the classical PDEs can’t be solved in closed form.

Another thing I didn’t know: Clairaut (from the “symmetry of mixed partial derivatives” fame) actually came up with the idea of the Fourier series before Fourier did; he did this in an applied setting.

Next talk Amie Wilkinson of Northwestern (soon to be University of Chicago) gave a talk about dynamical systems. She is one of those who has publication in the finest journals that mathematics has to offer (stellar).

The whole talk was pretty good. Highlights: she mentioned Henri Poincare and how he worked on the 3-body problem (one massive body, one medium body, and one tiny body that didn’t exert gravitational force on the other bodies). This creates a 3-dimensional system whose dynamics live in 3-space (the system space is, of course, has much higher dimension). Now consider a closed 2 dimensional manifold in that space and a point on that manifold. Now study the orbit of that point under the dynamical system action. Eventually, that orbit intersects the 2 dimensional manifold again. The action of moving from the first point to the first intersection point actually describes a motion ON THE TWO MANIFOLD and if we look at ALL intersections, we get a the orbit of that point, considered as an action on the two dimensional manifold.

So, in some sense, this two manifold has an “inherited” action on it. Now if we look at, say, a square on that 2-dimensional manifold, it was proved that this square comes back in a “folded” fashion: this is the famed “Smale Horseshoe map“:

Other things: she mentioned that there are dynamical systems that are stable with respect to perturbations that have unstable orbits (with respect to initial conditions) and that these instabilities cannot be perturbed away; they are inherent to the system. There are other dynamical systems (with less stability) that have this property as well.

There is, of course, much more. I’ll link to the lecture materials when I find them.

Last morning Talk
Bernd Sturmfels on Tropical Mathematics
Ok, quickly, if you have a semi-ring (no additive inverses) with the following operations:
min and (check that the operations distribute), what good would it be? Why would you care about such a beast?

Answer: many reasons. This sort of object lends itself well to things like matrix operations and is used for things such as “least path” problems (dynamic programming) and “tree metrics” in biology.

Think of it this way: if one is considering, say, an “order n” technique in numerical analysis, then the products of the error terms adds to the order, and the sum of the errors gives the, ok, maximum of the two summands (very similar).

The PDF of the slides in today’s lecture can be found here.

MathFest Day Three (Lexington 2011)

I left after the second large lecture and didn’t get a chance to blog about them before now.

But what I saw was very good.

The early lecture was by Lauren Ancel Meyers (Texas-Austin) on Mathematical Approaches to Infectious Disease and Control This is one of those talks where I wish I had access to the slides; they were very useful.

She started out by giving a brief review of the classical SIR model of the spread of a disease which uses the mass action principle (from science) that says that the rate of of change of those infected with a disease is proportional to the product of those who are susceptible to the disease and those who can transmit the disease: . (this actually came from chemistry). Of course, those who are infected either recover or die; this action reduces the number infected. Of course, the number of susceptible also drop.

This leads to a system of differential equations. The basic reproduction number is significant:
where is the recovery rate and 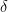is the death rate. Note: if then the disease will die off; if it is greater than 1 we have a pandemic. We can reduce this by reducing 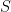(vaccination or quarantine), increasing recovery or, yes, increasing the death rate (as we do with livestock; remember the massive poultry slaughters to stop the spread of flu).

Of course, this model assumes that the infected organisms contact others at random and have equal probabilities of spreading, that the virus doesn’t evolve, etc.

So this model had to be improved on; methods from percolation theory were developed.

So many factors had to be taken into account such as: how much vaccine is there to spread? How far along is the outbreak? (at first children get it; then adults). How severe is the consequences? (we don’t want the virus to evolve to a more dangerous, more resistant form).

Note that the graph model of transmission is dynamic; it can actually change with time.

Of special interest: one can recover the rate of infections of the various strains (and the strains vary from season to season) by looking at the number of times flu related words were searched for on Google. The graph overlap (search rate versus reported cases) was stunning; the only exception is when a scare occurred; then the word search rate lead the actual cases, but that happened only once (2009). Note also that predictions of what will happen get better with a shorter time window (not a surprise).

There was much more in the talk; for example the role of the location of the providers of vaccines was discussed (what is the optimal way to spread out the availability of a given vaccine?)

Manjur Bhargava, Lecture III
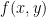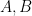First, he noted that in the case where was cubic, that there is always a rational change of variable to put the curve into the following form: where are integers that have the following property: if 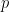is any prime where divides 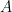then does NOT divide . So this curve can be denoted as .

Also, there are two “generic” cases of curves depending on whether the cubic in has only one real root or three real roots.

This is a catalog of elliptical algebraic curves of the form taken from here. The everywhere smooth curves are considered; the ones with a disconnected graph are said to have “an egg”; those are the ones in which the cubic in has three real roots. In the connected case, the cubic has only one; remember that these are genus one curves; we are seeing a slice of a torus in 4-space (a space with two complex dimensions) in the plane.

Also recall that the rational points on the curve may be finite or infinite. It turns out that the rational points (both coordinates rational) have a group structure (this is called the “divisor class group” in algebraic geometry). This group has a structure that can be understood by a simple geometric construction in the plane, though checking that the operation is associative can be very tedious.

I’ll give a description of the group operation and provide an elementary example:

First, note that if is a point on an elliptical curve, then so is (note: the on the left hand side of the defining equation). That is important. Also note that we will restrict ourselves to smooth curves (that have a well defined tangent line).

The elements of our group will be the rational points of the curve (if any?) along with the point at infinity. If I will denote .

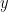The operation: if are rational points on the curve, construct the line with equation Substitute this into and note that we now have a cubic equation in that has two rational solutions; hence there must be a third rational solution . Associated to that value is two values (possibly double if the 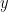value is zero). Call that point on the curve 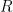then define where is the reflection of 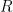about the axis.

Note the following: that this operation commutes is immediate. If one adds a point to itself, one uses the tangent line as the line through two points; note that such a line might not hit the curve a third time. If such a line is vertical (parallel to the 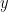axis) the result is said to be “0” (the point at infinity); if the line is not vertical but still misses the rest of the curve, it is counted three times; that is: . Here are the situations:

Of course, is the group identity. Associativity is difficult to check directly (elementary algebra but very tedious; perhaps 3-4 pages of it?).

Since the group is Abelian, if the group is finite it must be isomorphic to where the second part is the torsion part and the number of infinite cyclic factors is the rank. The rank turns out to be the geometric rank; that is, the minimum number of points required to obtain all of the rational points (infinite number) of the curve. Let 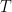be the torsion subgroup; Mazur proved that .

Let’s look at an example of a subgroup of such a curve: let the curve be given by It is easy to see that are all rational points. Let’s see how these work: so this point has order 2. But there is also some interesting behavior: note that which implies that So the tangent line through and are both horizontal; that means that both of these points have order 3. Note also that as the tangent line runs through the point . Similarly So, we can see that have order 6, have order 3 and has order 2. So there is an isomorphism 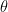where where the integers are mod 6.

So, we’ve shown a finite Abelian subgroup of the group of rationals of this curve. It turns out that these are the only rational points; here all we get is the torsion group. This curve has rank zero (not obvious).

Note: the group of rationals for is isomorphic to though this isn’t obvious.

The generator of the term is and generates the the torsion term.

History note Some of this was tackled by computers many years ago (Birch, Swinnerton-Dyer). Because computers were so limited in those days, the code had to be very efficient and therefore people had to do quite a bit of work prior to putting it into code; evidently this lead to progress. The speaker joked that such progress might not have been so quickly today due to better computers!

If one looks at where 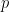is prime, we should have about 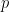points on the curve. So we’d expect that . If there are a lot of rational points on the curve, most of these points would correspond to points. So there is a conjecture by Birch, Swinnerton-Dyer:
where is the rank.

Yes, this is hard; win one million US dollars if you prove it. 🙂

Back to the curves: there are ways of assigning “heights” to these curves; some include:
or

Given this ordering, what are average sizes of ranks?
Katz-Sarnak: half have rank 0, half have rank 1. It was known that average ranks are bounded; previous results had the bound at 2.3, 2, 1.79, assuming that the Generalized Riemann Hypothesis and the Birch, Swinnerton-Dyer conjecture were asssumed.

The speaker and his students got some results without making these large assumptions:

Result 1: when is ordered by height, the average rank is less than 1.
Result 2: A positive portion (10 percent, at least) have rank 0.
Result 3: at least 80 percent have rank 0 or 1.
Corollary: the BSD is true for a positive proportion of elliptic curves;

The speaker (with his student) proved results 1, 2, and 3 and then worked backwards on the existing “BSD true implies X” results to show that BSD was true for a positive proportion of the elliptic curves.

MathFest Day 2 (2011: Lexington, KY)

I went to the three “big” talks in the morning.
Dawn Lott’s talk was about applied mathematics and its relation to the study of brain aneurysms; in particular the aneurysm model was discussed (partial differential equations with a time coordinate and stresses in the radial, circumference and latitudinal directions were modeled).

There was also modeling of the clipping procedure (where the base of the aneurysm was clipped with a metal clip); various clipping strategies were investigated (straight across? diagonal?). One interesting aspect was that the model of the aneurysm was discussed; what shape gave the best results?

Note: this is one procedure that was being modeled:

Next, Bhargava gave his second talk (on rational points on algebraic curves)
It was excellent. In the previous lecture, we saw that a quadratic curve either has an infinite number of rational points or zero rational points. Things are different with a cubic curve.

For example, has exactly one rational point (namely (0,0) ) but has an infinite number! It turns out that the number of rational points an algebraic curve has is related to the genus of the graph of the curve in (where one uses complex values for both variables). The surface is a punctured multi-holed torus of genus with the punctures being “at infinity”.

The genus is as follows: 0 if the degree is 1 or 2, 1 if the degree is 3, and greater than 1 if the degree is 4 or higher. So what about the number of rational points:
0 or finite if the genus is zero
finite if the genus is strictly greater than 1 (Falting’s Theorem; 1983)
indeterminate if the genus is 1. Hence much work is done in this area.

No general algorithm is known to make the determination if the curve is cubic (and therefore of genus 1)

Note: the set of rational points has a group structure.

Note: a rational cubic has a rational change of variable which changes the curve to elliptic form:
Weierstrauss form: where are integers.
Hence this is the form that is studied.
Sometimes the rational points can be found in the following way (example: :
note: this curve is symmetric about the axis.
is a rational point. So is . This line intersects the curve in a third point; this line and the cubic form a cubic in with two rational roots; hence the third must be rational. So we get a third rational point. Then we use to obtain another line and still another rational point; we keep adding rational points in this manner.

This requires proof, but eventually we get all of the rational points in this manner.

The minimum number of “starting points” that we need to find the rational points is called the “rank” of the curve. Our curve is of rank 1 since we really needed only (which, after reflecting, yields a line and a third rational point).

Mordell’s Theorem: every cubic is of finite rank, though it is unknown (as of this time) what the maximum rank is (maximum known example: rank 28), what an expected size would be, or even if “most” are rank 0 or rank 1.

Note: rank 0 means only a finite number of rational points.

Smaller talks
I enjoyed many of the short talks. Of note:
there was a number theory talk by Jay Schiffman in which different conjectures of the following type were presented: if is some sequence of positive integers and we look at the series of partial sums, or partial products (plus or minus some set number), what can we say about the number of primes that we obtain?

Example: Consider the Euclid product of primes (used to show that there is no largest prime number)
etc. It is unknown if there is a largest prime in the sequence .

Another good talk was given by Charlie Smith. It was about the proofs of the irrationality of various famous numbers; it was shown that many of the proofs follow a similar pattern and use a series of 3 techniques/facts that the presenter called “rabbits”. I might talk about this in a later post.

Another interesting talk was given by Jack Mealy. It was about a type of “hyper-hyperbolic” geometry called a “Snell geometry”. Basically one sets up the plane and then puts in a smooth closed boundary curve (say, a line or a sphere). One then declares that the geodesics are those that result from a straight lines…that stay straight until they hit the boundary; they then obey the Snell’s law from physics with respect to the normal of the boundary surface; the two rays joined together from the geodesic in the new geometry. One can do this with, say, a concentric series of circles.

If one arranges the density coefficient in the correct manner, one’s density (in terms of area) can be made to increase as one goes outward; this can lead to interesting area properties of triangles.

Blogging MathFest, 2011 (Lexington, KY)

This is what I am talking about:

I started the day by attending three large lectures:
Laura DeMarco, University of Illinois at Chicago who spoke about dynamical systems (that result from complex polynomials; for example if is a function of the complex plane, one can talk about the orbit of a point . One can then talk about sets of points and This is called the Filled Julia Set.

Ed Burger of Williams (a graduate school classmate of mine who made good) gave the second; he talked about Fibonacci numbers and their relation to irrational ratios (which can be obtained by continued fractions) and various theorems which say that natural numbers can be written uniquely as specified sums of such gadgets.

Lastly Manjul Bhargava of Princeton (who is already full professor though he is less than half my age; he was an Andrew Wiles student) gave a delightful lecture on algebraic curves.

What I noted: all three of these mathematicians are successful enough to be arrogant (especially the third). They could have blown us all away. Yes, they took the time and care to give presentations that actually taught us something.

Of the three, I was the most intrigued by the last one, so I’ll comment on the mathematics.

You’ve probably heard that a Pythagorean triple is a triple of integers such that . For now, we’ll limit ourselves to primitive triples; that is, we’ll assume that have no common factor.

You might have heard that any Pythagorean triple is of the form: for integers. It is true that being defined that way leads to a Pythagorean triple, but why do ALL Pythagorean triples come in this form?

One way to see this is to look at an algebraic curve; in this case, the curve corresponding to . Why? Start with and divide both sides by to obtain One then notes that one is now reduced to looking to rational solutions to (a rational solution to this can be put in the form by getting a common denominator).

We now wish to find all rational points (both coordinates rational) on the circle; clearly is one of them.
Easy claim: if is such a rational point, then the line from to has rational slope.
Not quite as easy claim: if a line running through has rational slope then the line intersects the circle in a rational point.
Verification: such a line has equation and intersects the circle in a point whose value satisfies . This is a quadratic that has rational coefficients and root hence the second root must also be rational. Let’s calculate the second root by doing division: . So the point of intersection has latex and . Both are rational.

Therefore, there is a one to one correspondence between rational slopes and rational points on the circle and all are of the form . Note: we obtain by letting go to infinity; use L’Hopital’s rule on the first coordinate). So if we have any Pythagorean triple then But is rational hence we write where are relatively prime integers. Just a bit of easy algebra reveals which gives us as required.

The point: the algebraic curve motivated the proof that all Pythagorean triples are of that form.

Note: we can extract even more: if latex is any quadratic rational curve (i. e., , all coefficients rational, and is any rational point and there is a line through of rational slope which intersects the curve in a second point (the quadratic nature forbids more than 2 points), the second point must also be rational. This follows by obtaining a quadratic in by substituting and obtaining a quadratic with rational coefficients that has one rational root.

Of course, it might be the case that there is no rational point to choose for . In fact, that is the case for

Why? Suppose there is a rational point on this curve with both fractions in lowest terms. We obtain Now let’s work Mod 4 (hint from the talk): note that in therefore the sum of two squares can only be 0, 1 or 2. The right hand side is either 3 or 0; equality means that both sides are zero. This means that are both even and therefore is divisible by 4 therefore either is even or is even.
Suppose is odd. Then is even and because is even, is even. This contradicts the fact that are relatively prime. If is odd, then because is even, is even. This contradicts the fact that are relatively prime. So both are even which means that are odd. Write where are odd (possibly 1). Then . Now if we obtain on the left hand side (sum of two odd numbers squared) which must be 2 mod 4. The right hand side is still only 3 or 0; this is impossible. Now if, say, then we get which means that the odd number is the difference of two even numbers. That too is impossible.

Hence contains no rational coordinates; that circle manages to miss that dense set.

The point of all of this is that algebraic curves can yield significant information about number theory.

Photos

This is the German Enigma Coding machine (with plug board) at the NSA booth.

This is another view of the Enigma

Edward Burger; I had some bad timing here.

Just prior to the first talk.