College Math Teaching

August 28, 2017

Integration by parts: why the choice of “v” from “dv” might matter…

Filed under: advanced mathematics, applications of calculus, calculus, density function, improper integrals — Tags: — collegemathteaching @ 3:28 pm

We all know the integration by parts formula: \int u dv = uv - \int v du though, of course, there is some choice in what v is; any anti-derivative will do. Well, sort of.

I thought about this as I’ve been roped into teaching an actuarial mathematics class (and no, I have zero training in this area…grrr…)

So here is the set up: let F_x(t) = P(0 \leq T_x \leq t) where T_x is the random variable that denotes the number of years longer a person aged x will live. Of course, F_x is a probability distribution function with density function f and if we assume that F is smooth and T_x has a finite expected value we can do the following: E(T_x) = \int^{\infty}_0 t f_x(t) dt and, in principle this integral can be done by parts….but…if we use u = t, dv = f_x(t), du = dt, v = F_x we have:

\

t(F_x(t))|^{\infty}_0 -\int^{\infty}_0 F_x(t) dt which is a big problem on many levels. For one, lim_{t \rightarrow \infty}F_x(t) = 1 and so the new integral does not converge..and the first term doesn’t either.

But if, for v = -(1-F_x(t)) we note that (1-F_x(t)) = S_x(t) is the survival function whose limit does go to zero, and there is usually the assumption that tS_x(t) \rightarrow 0 as t \rightarrow \infty

So we now have: -(S_x(t) t)|^{\infty}_0 + \int^{\infty}_0 S_x(t) dt = \int^{\infty}_0 S_x(t) dt = E(T_x) which is one of the more important formulas.

August 1, 2017

Numerical solutions to differential equations: I wish that I had heard this talk first

Filed under: academia, advanced mathematics, conference, differential equations, numerical methods, numerical solution of differential equations — collegemathteaching @ 4:40 pm

The MAA Mathfest in Chicago was a success for me. I talked about some other talks I went to; my favorite was probably the one given by Douglas Arnold. I wish I had had this talk prior to teaching numerical analysis for the fist time.

Confession: my research specialty is knot theory (a subset of 3-manifold topology); all of my graduate program classes have been in pure mathematics. I last took numerical analysis as an undergraduate in 1980 and as a “part time, not taking things seriously” masters student in 1981 (at UTSA of all places).

In each course…I. Made. A. “C”.

Needless to say, I didn’t learn a damned thing, even though both professors gave decent courses. The fault was mine.

But…I was what my department had, and away I went to teach the course. The first couple of times, I studied hard and stayed maybe 2 weeks ahead of the class.
Nevertheless, I found the material fascinating.

When it came to understanding how to find a numerical approximation to an ordinary differential equation (say, first order), you have: y' = f(t,y) with some initial value for both y'(0), y(0) . All of the techniques use some sort of “linearization of the function” technique to: given a step size, approximate the value of the function at the end of the next step. One chooses a step size, and some sort of schemes to approximate an “average slope” (e. g. Runga-Kutta is one of the best known).

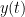This is a lot like numerical integration, but in integration, one knows y'(t) for all values; here you have to infer y'(t) from previous approximations of %latex y(t) $. And there are things like error (often calculated by using some sort of approximation to y(t) such as, say, the Taylor polynomial, and error terms which are based on things like the second derivative.

And yes, I faithfully taught all that. But what was unknown to me is WHY one might choose one method over another..and much of this is based on the type of problem that one is attempting to solve.

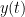And this is the idea: take something like the Euler method, where one estimates y(t+h) \approx y(t) + y'(t)h . You repeat this process a bunch of times thereby obtaining a sequence of approximations for y(t) . Hopefully, you get something close to the “true solution” (unknown to you) (and yes, the Euler method is fine for existence theorems and for teaching, but it is too crude for most applications).

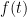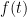But the Euler method DOES yield a piecewise linear approximation to SOME f(t) which might be close to y(t) (a good approximation) or possibly far away from it (a bad approximation). And this f(t) that you actually get from the Euler (or other method) is important.

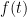It turns out that some implicit methods (using an approximation to obtain y(t+h) and then using THAT to refine your approximation can lead to a more stable system of f(t) (the solution that you actually obtain…not the one that you are seeking to obtain) in that this system of “actual functions” might not have a source or a sink…and therefore never spiral out of control. But this comes from the mathematics of the type of equations that you are seeking to obtain an approximation for. This type of example was presented in the talk that I went to.

In other words, we need a large toolbox of approximations to use because some methods work better with certain types of problems.

I wish that I had known that before…but I know it now. 🙂

Big lesson that many overlook: math is hard

Filed under: advanced mathematics, conference, editorial, mathematician, mathematics education — Tags: — collegemathteaching @ 11:43 am

First of all, it has been a very long time since I’ve posted something here. There are many reasons that I allowed myself to get distracted. I can say that I’ll try to post more but do not know if I will get it done; I am finishing up a paper and teaching a course that I created (at the request of the Business College), and we have a record enrollment..many of the new students are very unprepared.

Back to the main topic of the post.

I just got back from MAA Mathfest and I admit that is one of my favorite mathematics conferences. Sure, the contributed paper sessions give you a tiny amount of time to present, but the main talks (and many of the simple talks) are geared toward those of us who teach mathematics for a living and do some research on the side; there are some mainstream “basic” subjects that I have not seen in 30 years!

That doesn’t mean that they don’t get excellent people for the main speaker; they do. This time, the main speaker was Dusa McDuff: someone who was a member of the National Academy of Sciences. (a very elite level!)

Her talk was on the basics of symplectec geometry (introductory paper can be found here) and the subject is, well, HARD. But she did an excellent job of giving the flavor of it.

I also enjoyed Erica Flapan’s talk on graph theory and chemistry. One of my papers (done with a friend) referenced her work.

I’ll talk about Douglas Arnold’s talk on “when computational math meets geometry”; let’s just say that I wish I had seen this lecture prior to teaching the “numerical solutions for differential equations” section of numerical analysis.

Well, it looks as if I have digressed yet again.

There were many talks, and some were related to the movie Hidden Figures. And the cheery “I did it and so can you” talks were extremely well attended…applause, celebration, etc.

The talks on sympletec geometry: not so well attended toward the end. Again, that stuff is hard.

And that is one thing I think that we miss when we encourage prospective math students: we neglect to tell them that research level mathematics is difficult stuff and, while some have much more talent for it than others, everyone has to think hard, has to work hard, and almost all of us will fail, quite a bit.

I remember trying to spend over a decade trying to prove something, only to fail and to see a better mathematician get the result. One other time I spent 2 years trying to “prove” something…and I couldn’t “seal the deal”. Good thing too, as what I was trying to prove was false..and happily I was able to publish the counterexample.

Blog at WordPress.com.