College Math Teaching

March 29, 2020

A change of variable to determine if growth is still exponential

Filed under: applications of calculus, applied mathematics, COVID19, differential equations — Tags: , — collegemathteaching @ 12:07 pm

This video is pretty good, and I thought that I’d add some equations to the explanation:

So, in terms of the mathematics, what is going on?

The graph they came up with is “new confirmed cases” on the y-axis (log scale) and total number of cases on the x-axis. Let’s see what this looks like for exponential growth.

Here, letting the total number of cases at time t be denoted by P(t) , the number of new cases is P'(t) , the first derivative.

In the case of exponential growth, P(t) = Ae^{kt} where k is positive.

P'(t) = Ake^{kt} which is what is being plotted on the y-axis. So with the change of variable we are letting u = Ae^{kt} and our new function is F(u) = ku , which, of course, is a straight line through the origin. That is, of course, IF the growth is exponential.

To get a feel for what this looks like, suppose we had polynomial growth; say P(t) = At^k . Then P'(t) =Akt^{k-1} = ak\frac{t^{k}}{t} =ak\frac{u}{u^{\frac{1}{k}}} =aku^{\frac{k-1}{k}} In the case of linear growth we’d have F(u) =ak (constant) and for, say, k = 3, F(u) =3au^{\frac{2}{3}} or a “concave down” function.

Now for the logistic situation in which the number of cases grows exponentially at first and then starts to level out to some steady state value, call it L, the relationship between the number of cases and the new number of cases looks like P'(t) = akP(L-P)) so our F(u) =aku(L-u) which is a quadratic which opens down.

Yes, this gets studied in differential equations class when we study autonomous differential equations.

Now for some graphs:

This is exponential growth vs. logistic growth; we get something similar to the latter when cases start to peak.

Here, I tweaked the logistic model to have the same derivative as the exponential model near t = 0 .

Here: we have linear growth P(t) = 5t vs the F(u) = 5

Here: cubic growth P(t) = 5t^3 vs. F(u) = 5u^{\frac{2}{3}}

March 26, 2020

My review lessons online

Filed under: applications of calculus, COVID19, differential equations, linear albegra — collegemathteaching @ 11:04 am

We had an extra week to prepare to teach online, so I put notes from the previous few weeks up in blog form:

Blog

Blog

Blog

That was quite a bit of work, but I did find some cool videos out there and embedded them in my lessons.

August 28, 2017

Integration by parts: why the choice of “v” from “dv” might matter…

Filed under: advanced mathematics, applications of calculus, calculus, density function, improper integrals — Tags: — collegemathteaching @ 3:28 pm

We all know the integration by parts formula: \int u dv = uv - \int v du though, of course, there is some choice in what v is; any anti-derivative will do. Well, sort of.

I thought about this as I’ve been roped into teaching an actuarial mathematics class (and no, I have zero training in this area…grrr…)

So here is the set up: let F_x(t) = P(0 \leq T_x \leq t) where T_x is the random variable that denotes the number of years longer a person aged x will live. Of course, F_x is a probability distribution function with density function f and if we assume that F is smooth and T_x has a finite expected value we can do the following: E(T_x) = \int^{\infty}_0 t f_x(t) dt and, in principle this integral can be done by parts….but…if we use u = t, dv = f_x(t), du = dt, v = F_x we have:

\

t(F_x(t))|^{\infty}_0 -\int^{\infty}_0 F_x(t) dt which is a big problem on many levels. For one, lim_{t \rightarrow \infty}F_x(t) = 1 and so the new integral does not converge..and the first term doesn’t either.

But if, for v = -(1-F_x(t)) we note that (1-F_x(t)) = S_x(t) is the survival function whose limit does go to zero, and there is usually the assumption that tS_x(t) \rightarrow 0 as t \rightarrow \infty

So we now have: -(S_x(t) t)|^{\infty}_0 + \int^{\infty}_0 S_x(t) dt = \int^{\infty}_0 S_x(t) dt = E(T_x) which is one of the more important formulas.

May 11, 2015

The hypervolume of the n-ball enclosed by a standard n-1 sphere

Filed under: analysis, applications of calculus, calculus, integrals, integration by substitution, pedagogy — Tags: , , , — collegemathteaching @ 12:08 am

I am always looking for interesting calculus problems to demonstrate various concepts and perhaps generate some interest in pure mathematics.
And yes, I like to “blow off some steam” by spending some time having some non-technical mathematical fun with elementary mathematics.

This post uses only:

1. Integration by parts and basic reduction formulas.
2. Trig substitution.
3. Calculation of volumes (and hyper volumes) by the method of cross sections.
4. Induction
5. Elementary arithmetic involving factorials.

The quest: find a formula that finds the (hyper)volume of the region \{(x_1, x_2, x_3,....x_k) | \sum_{i=1}^k x_i^2 \leq R^2 \} \subset R^k

We will assume that the usual tools of calculus work as advertised.

Start. If we done the (hyper)volume of the k-ball by 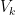V_k we will start with the assumption that V_1 = 2R ; that is, the distance between the endpoints of [-R,R] is 2R.

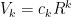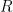Step 1: we show, via induction, that V_k =c_kR^k where c_k is a constant and R is the radius.

Our proof will be inefficient for instructional purposes.

We know that 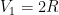V_1 =2R hence the induction hypothesis holds for the first case and 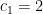c_1 = 2 . We now go to show the second case because, for the beginner, the technique will be easier to follow further along if we do the 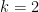k = 2 case.

Yes, I know that you know that V_2 = \pi R^2 and you’ve seen many demonstrations of this fact. Here is another: let’s calculate this using the method of “area by cross sections”. Here is x^2 + y^2 = R^2 with some y = c cross sections drawn in.

crosssections

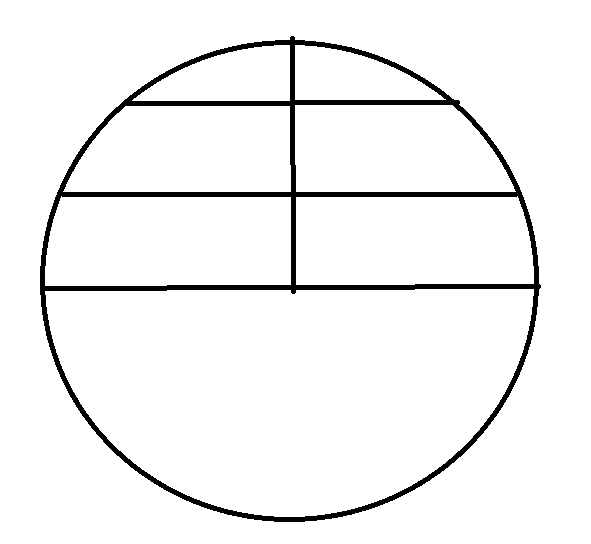
Now do the calculation by integrals: we will use symmetry and only do the upper half and multiply our result by 2. At each y = y_c level, call the radius from the center line to the circle R(y) so the total length of the “y is constant” level is 2R(y) and we “multiply by thickness “dy” to obtain V_2 = 4 \int^{y=R}_{y=0} R(y) dy .

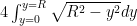
But remember that the curve in question is x^2 + y^2 = R^2 and so if we set x = R(y) we have R(y) = \sqrt{R^2 -y^2} and so our integral is 4 \int^{y=R}_{y=0}\sqrt{R^2 -y^2} dy

Now this integral is no big deal. But HOW we solve it will help us down the road. So here, we use the change of variable (aka “trigonometric substitution”): y = Rsin(t), dy =Rcos(t) to change the integral to:

4 \int^{\frac{\pi}{2}}_0 R^2 cos^2(t) dt = 4R^2 \int^{\frac{\pi}{2}}_0 cos^2(t) dt therefore

V_2 = c_2 R^2 where:

c_2 = 4\int^{\frac{\pi}{2}}_0 cos^2(t)

Yes, I know that this is an easy integral to solve, but I first presented the result this way in order to make a point.

Of course, c_2 = 4\int^{\frac{\pi}{2}}_0 cos^2(t) = 4\int^{\frac{\pi}{2}}_0 \frac{1}{2} + \frac{1}{2}cos(2t) dt = \pi

Therefore, V_2 =\pi R^2 as expected.

Exercise for those seeing this for the first time: compute c_3 and V_3 by using the above methods.

Inductive step: Assume V_k = c_kR^k Now calculate using the method of cross sections above (and here we move away from x-y coordinates to more general labeling):

V_{k+1} = 2\int^R_0 V_k dy = 2 \int^R_0 c_k (R(x_{k+1})^k dx_{k+1} =c_k 2\int^R_0 (R(x_{k+1}))^k dx_{k+1}

Now we do the substitutions: first of all, we note that 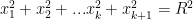x_1^2 + x_2^2 + ...x_{k}^2 + x_{k+1}^2 = R^2 and so

x_1^2 + x_2^2 ....+x_k^2 = R^2 - x_{k+1}^2 . Now for the key observation: x_1^2 + x_2^2 ..+x_k^2 =R^2(x_{k+1}) and so R(x_{k+1}) = \sqrt{R^2 - x_{k+1}^2}

Now use the induction hypothesis to note:

V_{k+1} = c_k 2\int^R_0 (R^2 - x_{k+1}^2)^{\frac{k}{2}} dx_{k+1}

Now do the substitution x_{k+1} = Rsin(t), dx_{k+1} = Rcos(t)dt and the integral is now:

V_{k+1} = c_k 2\int^{\frac{\pi}{2}}_0 R^{k+1} cos^{k+1}(t) dt = c_k(2 \int^{\frac{\pi}{2}}_0 cos^{k+1}(t) dt)R^{k+1} which is what we needed to show.

In fact, we have shown a bit more. We’ve shown that c_1 = 2 =2 \int^{\frac{\pi}{2}}_0(cos(t))dt, c_2 = 2 \cdot 2\int^{\frac{\pi}{2}}_0 cos^2(t) dt = c_1 2\int^{\frac{\pi}{2}}_0 cos^2(t) dt and, in general,

c_{k+1} = c_{k}c_{k-1}c_{k-2} ....c_1(2 \int^{\frac{\pi}{2}}_0 cos^{k+1}(t) dt) = 2^{k+1} \int^{\frac{\pi}{2}}_0(cos^{k+1}(t))dt \int^{\frac{\pi}{2}}_0(cos^{k}(t))dt \int^{\frac{\pi}{2}}_0(cos^{k-1}(t))dt .....\int^{\frac{\pi}{2}}_0(cos(t))dt

Finishing the formula

We now need to calculate these easy calculus integrals: in this case the reduction formula:

\int cos^n(x) dx = \frac{1}{n}cos^{n-1}sin(x) + \frac{n-1}{n} \int cos^{n-2}(x) dx is useful (it is merely integration by parts). Now use the limits and elementary calculation to obtain:

\int^{\frac{\pi}{2}}_0 cos^n(x) dx = \frac{n-1}{n} \int^{\frac{\pi}{2}}_0 cos^{n-2}(x)dx to obtain:

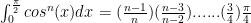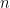\int^{\frac{\pi}{2}}_0 cos^n(x) dx = (\frac{n-1}{n})(\frac{n-3}{n-2})......(\frac{3}{4})\frac{\pi}{4} if n is even and:
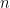\int^{\frac{\pi}{2}}_0 cos^n(x) dx = (\frac{n-1}{n})(\frac{n-3}{n-2})......(\frac{4}{5})\frac{2}{3} if n is odd.

Now to come up with something resembling a closed formula let’s experiment and do some calculation:

Note that 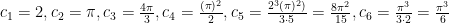c_1 = 2, c_2 = \pi, c_3 = \frac{4 \pi}{3}, c_4 = \frac{(\pi)^2}{2}, c_5 = \frac{2^3 (\pi)^2)}{3 \cdot 5} = \frac{8 \pi^2}{15}, c_6 = \frac{\pi^3}{3 \cdot 2} = \frac{\pi^3}{6} .

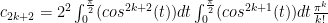
So we can make the inductive conjecture that c_{2k} = \frac{\pi^k}{k!} and see how it holds up: c_{2k+2} = 2^2 \int^{\frac{\pi}{2}}_0(cos^{2k+2}(t))dt \int^{\frac{\pi}{2}}_0(cos^{2k+1}(t))dt \frac{\pi^k}{k!}

= 2^2 ((\frac{2k+1}{2k+2})(\frac{2k-1}{2k})......(\frac{3}{4})\frac{\pi}{4})((\frac{2k}{2k+1})(\frac{2k-2}{2k-1})......\frac{2}{3})\frac{\pi^k}{k!}

Now notice the telescoping effect of the fractions from the 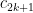c_{2k+1} factor. All factors cancel except for the (2k+2) in the first denominator and the 2 in the first numerator, as well as the \frac{\pi}{4} factor. This leads to:

c_{2k+2} = 2^2(\frac{\pi}{4})\frac{2}{2k+2} \frac{\pi^k}{k!} = \frac{\pi^{k+1}}{(k+1)!} as required.

Now we need to calculate 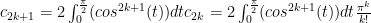c_{2k+1} = 2\int^{\frac{\pi}{2}}_0(cos^{2k+1}(t))dt c_{2k} = 2\int^{\frac{\pi}{2}}_0(cos^{2k+1}(t))dt \frac{\pi^k}{k!}

= 2 (\frac{2k}{2k+1})(\frac{2k-2}{2k-1})......(\frac{4}{5})\frac{2}{3}\frac{\pi^k}{k!} = 2 (\frac{(2k)(2k-2)(2k-4)..(4)(2)}{(2k+1)(2k-1)...(5)(3)} \frac{\pi^k}{k!}

To simplify this further: split up the factors of the k! in the denominator and put one between each denominator factor:

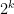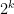= 2 (\frac{(2k)(2k-2)(2k-4)..(4)(2)}{(2k+1)(k)(2k-1)(k-1)...(3)(5)(2)(3)(1)} \pi^k Now multiply the denominator by 2^k and put one factor with each k-m factor in the denominator; also multiply by 2^k in the numerator to obtain:

(2) 2^k (\frac{(2k)(2k-2)(2k-4)..(4)(2)}{(2k+1)(2k)(2k-1)(2k-2)...(6)(5)(4)(3)(2)} \pi^k Now gather each factor of 2 in the numerator product of the 2k, 2k-2…

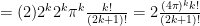= (2) 2^k 2^k \pi^k \frac{k!}{(2k+1)!} = 2 \frac{(4 \pi)^k k!}{(2k+1)!} which is the required formula.

So to summarize:

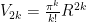
V_{2k} = \frac{\pi^k}{k!} R^{2k}

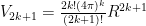
V_{2k+1}= \frac{2 k! (4 \pi)^k}{(2k+1)!}R^{2k+1}

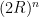Note the following: lim_{k \rightarrow \infty} c_{k} = 0 . If this seems strange at first, think of it this way: imagine the n-ball being “inscribed” in an n-cube which has hyper volume (2R)^n . Then consider the ratio \frac{2^n R^n}{c_n R^n} = 2^n \frac{1}{c_n} ; that is, the n-ball holds a smaller and smaller percentage of the hyper volume of the n-cube that it is inscribed in; note the 2^n corresponds to the number of corners in the n-cube. One might see that the rounding gets more severe as the number of dimensions increases.

One also notes that for fixed radius R, lim_{n \rightarrow \infty} V_n = 0 as well.

There are other interesting aspects to this limit: for what dimension 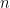n does the maximum hypervolume occur? As you might expect: this depends on the radius involved; a quick glance at the hyper volume formulas will show why. For more on this topic, including an interesting discussion on this limit itself, see Dave Richardson’s blog Division by Zero. Note: his approach to finding the hyper volume formula is also elementary but uses polar coordinate integration as opposed to the method of cross sections.

August 31, 2014

The convolution integral: do some examples in Calculus III or not?

Filed under: applications of calculus, applied mathematics, calculus, integrable function, integrals, Uncategorized — Tags: , — collegemathteaching @ 11:31 pm

For us, calculus III is the most rushed of the courses, especially if we start with polar coordinates. Getting to the “three integral theorems” is a real chore. (ok, Green’s, Divergence and Stoke’s theorem is really just \int_{\Omega} d \sigma = \int_{\partial \Omega} \sigma but that is the subject of another post)

But watching this lecture made me wonder: should I say a few words about how to calculate a convolution integral?

Note: I’ve discussed a type of convolution integral with regards to solving differential equations here.

In the context of Fourier Transforms, the convolution integral is defined as it was in analysis class: f*g = \int^{\infty}_{-\infty} f(x-t)g(t) dt . Typically, we insist that the functions be, say, L^1 and note that it is a bit of a chore to show that the convolution of two L^1 functions is L^1 ; one proves this via the Fubini-Tonelli Theorem.

(The straight out product of two L^1 functions need not be L^1 ; e.g, consider f(x) = \frac {1}{\sqrt{x}} for x \in (0,1] and zero elsewhere)

So, assuming that the integral exists, how do we calculate it? Easy, you say? Well, it can be, after practice.

But to test out your skills, let f(x) = g(x) be the function that is 1 for x \in [\frac{-1}{2}, \frac{1}{2}] and zero elsewhere. So, what is f*g ???

So, it is easy to see that f(x-t)g(t) only assumes the value of 1 on a specific region of the (x,t) plane and is zero elsewhere; this is just like doing an iterated integral of a two variable function; at least the first step. This is why it fits well into calculus III.

f(x-t)g(t) = 1 for the following region: (x,t), -\frac{1}{2} \le x-t \le \frac{1}{2}, -\frac{1}{2} \le t \le \frac{1}{2}

This region is the parallelogram with vertices at (-1, -\frac{1}{2}), (0, -\frac{1}{2}), (0 \frac{1}{2}), (1, \frac{1}{2}) .

convolutiondraw

Now we see that we can’t do the integral in one step. So, the function we are integrating f(x-t)f(t) has the following description:

f(x-t)f(t)=\left\{\begin{array}{c} 1,x \in [-1,0], -\frac{1}{2} t \le \frac{1}{2}+x \\ 1 ,x\in [0,1], -\frac{1}{2}+x \le t \le \frac{1}{2} \\ 0 \text{ elsewhere} \end{array}\right.

So the convolution integral is \int^{\frac{1}{2} + x}_{-\frac{1}{2}} dt = 1+x for x \in [-1,0) and \int^{\frac{1}{2}}_{-\frac{1}{2} + x} dt = 1-x for x \in [0,1] .

That is, of course, the tent map that we described here. The graph is shown here:

tentmapgraph

So, it would appear to me that a good time to do a convolution exercise is right when we study iterated integrals; just tell the students that this is a case where one “stops before doing the outside integral”.

August 21, 2014

Calculation of the Fourier Transform of a tent map, with a calculus tip….

Filed under: applications of calculus, applied mathematics, basic algebra, calculus, elementary mathematics, integrals, integration by substitution, science — Tags: , , — collegemathteaching @ 6:52 pm

I’ve been following these excellent lectures by Professor Brad Osgood of Stanford. As an aside: yes, he is dynamite in the classroom, but there is probably a reason that Stanford is featuring him. 🙂

And yes, his style is good for obtaining a feeling of comradery that is absent in my classroom; at least in the lower division “service” classes.

This lecture takes us from Fourier Series to Fourier Transforms. Of course, he admits that the transition here is really a heuristic trick with symbolism; it isn’t a bad way to initiate an intuitive feel for the subject though.

However, the point of this post is to offer a “algebra of calculus trick” for dealing with the sort of calculations that one might encounter.

By the way, if you say “hey, just use a calculator” you will be BANNED from this blog!!!! (just kidding…sort of. 🙂 )

So here is the deal: let f(x) represent the tent map: the support of f is [-1,1] and it has the following graph:

tentmapgraph

The formula is: f(x)=\left\{\begin{array}{c} x+1,x \in [-1,0) \\ 1-x ,x\in [0,1] \\ 0 \text{ elsewhere} \end{array}\right.

So, the Fourier Transform is F(f) = \int^{\infty}_{-\infty} e^{-2 \pi i st}f(t)dt = \int^0_{-1} e^{-2 \pi i st}(1+t)dt + \int^1_0e^{-2 \pi i st}(1-t)dt

Now, this is an easy integral to do, conceptually, but there is the issue of carrying constants around and being tempted to make “on the fly” simplifications along the way, thereby leading to irritating algebraic errors.

So my tip: just let a = -2 \pi i s and do the integrals:

\int^0_{-1} e^{at}(1+t)dt + \int^1_0e^{at}(1-t)dt and substitute and simplify later:

Now the integrals become: \int^{1}_{-1} e^{at}dt + \int^0_{-1}te^{at}dt - \int^1_0 te^{at} dt.
These are easy to do; the first is merely \frac{1}{a}(e^a - e^{-a}) and the next two have the same anti-derivative which can be obtained by a “integration by parts” calculation: \frac{t}{a}e^{at} -\frac{1}{a^2}e^{at}; evaluating the limits yields:

-\frac{1}{a^2}-(\frac{-1}{a}e^{-a} -\frac{1}{a^2}e^{-a}) - (\frac{1}{a}e^{a} -\frac{1}{a^2}e^a)+ (-\frac{1}{a^2})

Add the first integral and simplify and we get: -\frac{1}{a^2}(2 - (e^{-a} -e^{a}) . NOW use a = -2\pi i s and we have the integral is \frac{1}{4 \pi^2 s^2}(2 -(e^{2 \pi i s} -e^{-2 \pi i s}) = \frac{1}{4 \pi^2 s^2}(2 - cos(2 \pi s)) by Euler’s formula.

Now we need some trig to get this into a form that is “engineering/scientist” friendly; here we turn to the formula: sin^2(x) = \frac{1}{2}(1-cos(2x)) so 2 - cos(2 \pi s) = 4sin^2(\pi s) so our answer is \frac{sin^2( \pi s)}{(\pi s)^2} = (\frac{sin(\pi s)}{\pi s})^2 which is often denoted as (sinc(s))^2 as the “normalized” sinc(x) function is given by \frac{sinc(\pi x)}{\pi x} (as we want the function to have zeros at integers and to “equal” one at x = 0 (remember that famous limit!)

So, the point is that using a made the algebra a whole lot easier.

Now, if you are shaking your head and muttering about how this calculation was crude that that one usually uses “convolution” instead: this post is probably too elementary for you. 🙂

October 16, 2013

Convincing calculus students that the symbols MEAN SOMETHING

Filed under: applications of calculus, calculus, integrals — collegemathteaching @ 12:04 am

On a recent exam, the first 5 questions were as follows:

Given the region bounded by x = \frac{1}{2}, x = 1, y = 0, y = \frac{1}{x}

1. Find the AREA enclosed by the region.

2. Find the volume obtained by revolving this area about the y axis (the line x = 0 ).

3. Find the volume obtained by revolving this area about the x axis (the line y = 0 ).

4. Find \bar{x} . (constant density lamina).

5. Find \bar{y} .

Many students did fine, though there were a couple who literally blanked out on how to integrate \frac{1}{x} .

But some…well expect a few errors. But there were some who put a factor of \pi in their answers to 4, 5, and…yes, even 1.

Evidently, I’ll have to give my “these symbols actually have MEANING” speech again.

Note: yes, there were some interesting symmetries here; perhaps some students didn’t believe their answers.

October 15, 2013

Hydrostatic force and work problems and …topology?

Filed under: applications of calculus, applied mathematics, calculus — Tags: , — collegemathteaching @ 3:54 pm

I just gave my second “calculus two” exam; the final two problems involved the following:

Suppose a trough with semi-circular ends is filled with water (say, length = 40 feet, radius = 5 feet).

1. How much work does one do in pumping all of the water to the top of the tank and out? (work against gravity only)

2. How much hydrostatic force is there against one of the semi-circular end plates?

trough

Assuming water is 62.5 pounds per gallon (I gave that to them):

1. Work = 62.5 \int^5_0 40x \sqrt{25 - x^2} dx ; of course, x is the distance a molecule of water is lifted and 40 \sqrt{25 - x^2} dx is the cross sectional volume of water.

2. Force = 62.5 \int^5_0 x \sqrt{25 - x^2} dx ; of coure, x is the depth of the water (hence 62.5 x is the pressure at that depth) and \sqrt{25 - x^2} dx is the area at depth x that the pressure is applied to.

The student can easily notice that the two answers differ by a factor of 40, which is the length of the trough.

So, what is the lesson here? Well, for one, I always envisioned a wall of a tank holding back a long mass of water. That isn’t correct; ONLY THE DEPTH matters. If the tank were a mile long or, say, an inch long, the pressure on the semi-circular ends would be the same. That runs counter to my intuition (which is clearly bad).

This lead me to think about the following: what if one were to put in a baffle between the two ends and the baffle was the same shape as the semi-circular ends. What would be the force on that plate?

Of course, the net force would be zero; there are two sides of the plate.

Now drop an open cylinder into the tank (think: a can with the top and bottom cut away). Clearly: zero force on the sides, right? Two sides, right?

Now, drop a Mobius band into the tank. A Mobius band has but one side. What is the force on it?

The key here: the Mobius band is one sided, but it is LOCALLY two sided; one can break the surface into tiny rectangles and note that the net force on each rectangle is zero as it is locally two sided. Hence zero total force on the one sided object.

July 12, 2013

An example to apply Bayes’ Theorem and multivariable calculus

Filed under: applications of calculus, applied mathematics, calculus, optimization, pedagogy, science, statistics — Tags: , — collegemathteaching @ 9:49 pm

I’ve thought a bit about the breast cancer research results and found a nice “application” exercise that might help teach students about Bayes Theorem, two-variable maximizing, critical points, differentials and the like.

I’ve been interested in the mathematics and statistics of the breast cancer screening issue mostly because it provided a real-life application of statistics and Bayes’ Theorem.

So right now, for women between 40-49, traditional mammograms are about 80 percent accurate in the sense that, if a woman who really has breast cancer gets a mammogram, the test will catch it about 80 percent of the time. The false positive rate is about 8 percent in that: if 100 women who do NOT have breast cancer get a mammogram, 8 of the mammograms will register a “positive”.
Since the breast cancer rate for women in this age group is about 1.4 percent, there will be many more false positives than true positives; in fact a woman in this age group who gets a “positive” first mammogram has about a 16 percent chance of actually having breast cancer. I talk about these issues here.

So, suppose you desire a “more accurate test” for breast cancer. The question is this: what do you mean by “more accurate”?

1. If “more accurate” means “giving the right answer more often”, then that is pretty easy to do.
Current testing is going to be wrong: if C means cancer, N means “doesn’t have cancer”, P means “positive test” and M means “negative test”, then the probability of being wrong is:
P(M|C)P(C) + P(P|N)P(N) = .2(.014) + .08(.986) = .08168. On the other hand, if you just declared EVERYONE to be “cancer free”, you’d be wrong only 1.4 percent of the time! So clearly that does not work; the “false negative” rate is 100 percent, though the “false positive” rate is 0.

On the other hand if you just told everyone “you have it”, then you’d be wrong 98.6 percent of the time, but you’d have zero “false negatives”.

So being right more often isn’t what you want to maximize, and trying to minimize the false positives or the false negatives doesn’t work either.

2. So what about “detecting more of the cancer that is there”? Well, that is where this article comes in. Switching to digital mammograms does increase detection rate but also increases the number of false positives:

The authors note that for every 10,000 women 40 to 49 who are given digital mammograms, two more cases of cancer will be identified for every 170 additional false-positive examinations.

So, what one sees is that if a woman gets a positive reading, she now has an 11 percent of actually having breast cancer, though a few more cancers would be detected.

Is this progress?

My whole point: saying one test is “more accurate” than another test isn’t well defined, especially in a situation where one is trying to detect something that is relatively rare.
Here is one way to look at it: let the probability of breast cancer be a , the probability of detection of a cancer be given by x and the probability of a false positive be given by y . Then the probability of a person actually having breast cancer, given a positive test is given by:
B(x,y) =\frac{ax}{ax + (1-a)y} ; this gives us something to optimize. The partial derivatives are:
\frac{\partial B}{\partial x}= \frac{(a)(1-a)y}{(ax+ (1-a)y)^2},\frac{\partial B}{\partial y}=\frac{(-a)(1-a)x}{(ax+ (1-a)y)^2} . Note that 1-a is positive since a is less than 1 (in fact, it is small). We also know that the critical point x = y =0 is a bit of a “duh”: find a single test that gives no false positives and no false negatives. This also shows us that our predictions will be better if y goes down (fewer false positives) and if x goes up (fewer false negatives). None of that is a surprise.

But of interest is in the amount of change. The denominators of each partial derivative are identical. The coefficients of the numerators are of the same magnitude; there are different signs. So the rate of improvement of the predictive value is dependent on the relative magnitudes of x , which is .8 for us, and y , which is .08. Note that x is much larger than y and x occurs in the numerator \frac{\partial B}{\partial y} . Hence an increase in the accuracy of the y factor (a decrease in the false positive rate) will have a greater effect on the accuracy of the test than a similar increase in the “false negative” accuracy.
Using the concept of differentials, we expect a change \Delta x = .01 leads to an improvement of about .00136 (substitute x = .8, y = .08 into the expression for \frac{\partial B}{\partial x} and multiply by .01. Similarly an improvement (decrease) of \Delta y = -.01 leads to an improvement of .013609.

You can “verify” this by playing with some numbers:

Current (x = .8, y = .08 ) we get B = .1243 . Now let’s change: x = .81, y = .08 leads to B = .125693
Now change: x = .8, y = .07 we get B = .139616

Bottom line: the best way to increase the predictive value of the test is to reduce the number of false positives, while staying the same (or improving) the percentage of “false negatives”. As things sit, the false positive rate is the bigger factor affecting predictive value.

July 1, 2013

Mathematics: aids the conceptual understanding of elementary physics

Filed under: applications of calculus, editorial, elementary mathematics, pedagogy, physics — collegemathteaching @ 4:52 pm

I was blogging about the topic of how “classroom knowledge” turns into “walking around knowledge” and came across an “elementary physics misconceptions” webpage at the University of Montana. It is fun, but it helped me realize how easy things can be when one thinks mathematically.

Example.

Screen shot 2013-07-01 at 11.25.49 AM

This becomes very easy if one does a bit of mathematics. Let m represent the mass of the object; F = 10 = ma implies that a = \frac{10}{m} which isn’t that important; we’ll just use a . Now putting into vector form we have \vec{a}(t) = a \vec{i}, \vec{v}(0) = V_i \vec{j}, \vec{s}(0) = \vec{0} . By elementary integration, obtain \vec{v} = at \vec{i} + V_i \vec{j} and integrate again to obtain \vec{s}(t) = \frac{1}{2}at^2\vec{i}+(V_i)t\vec{j} which has parametric equations x(t) = \frac{a}{2}t^2, y(t) = V_i t which has a “sideways parabola” as a graph.

Let’s look at another example:

Screen shot 2013-07-01 at 11.40.26 AM

So what is going on? Force F = \frac{d}{dt}(mv) = \frac{dm}{dt}v + m\frac{dv}{dt} = 0 . The first term is thrust and is against the direction of acceleration. So we have:1000 = m\frac{dv}{dt} which, upon integration, implies that \frac{1000}{m} t + v_0 = v(t) and so we see that the rocket continues to speed up at a constant acceleration.

These problems are easier with mathematics, aren’t they? 🙂

Older Posts »

Blog at WordPress.com.