College Math Teaching

January 20, 2014

A bit more prior to admin BS

Filed under: advanced mathematics, applied mathematics, physics, popular mathematics, quantum mechanics, science, sequences, series — collegemathteaching @ 5:35 pm

One thing that surprised me about the professor’s job (at a non-research intensive school; we have a modest but real research requirement, but mostly we teach): I never knew how much time I’d spend doing tasks that have nothing to do with teaching and scholarship. Groan….how much of this do I tell our applicants that arrive on campus to interview? 🙂

But there is something mathematical that I want to talk about; it is a follow up to this post. It has to do with what string theorist tell us: \sum^{\infty}_{k = 1} k = -\frac{1}{12} . Needless to say, they are using a non-standard definition of “value of a series”.

Where I think the problem is: when we hear “series” we think of something related to the usual process of addition. Clearly, this non-standard assignment doesn’t related to addition in the way we usually think about it.

So, it might make more sense to think of a “generalized series” as a map from the set of sequences of real numbers (or: the infinite dimensional real vector space) to the real numbers; the usual “limit of partial sums” definition has some nice properties with respect to sequence addition, scalar multiplication and with respect to a “shift operation” and addition, provided we restrict ourselves to a suitable collection of sequences (say, those whose traditional sum of components are absolutely convergent).

So, this “non-standard sum” can be thought of as a map f:V \rightarrow R^1 where f(\{1, 2, 3, 4, 5,....\}) \rightarrow -\frac{1}{12} . That is a bit less offensive than calling it a “sum”. 🙂

August 12, 2013

Today’s Google Doodle

Filed under: quantum mechanics — Tags: , — collegemathteaching @ 6:22 pm

Screen shot 2013-08-12 at 8.14.27 AM

1. What is that device on the left of the equals sign?
2. What is with the \sqrt{2} ???

Note: I’d prefer |\Psi> = p(|"live cat">) + (1-p)(|"dead cat">) where 0 \le p \le 1
(joke)

Yes, it is August 12.

August 14, 2012

A quick thought on the “Interdisciplinary” focus on the undergraduate level

Filed under: academia, calculus, editorial, integrals, mathematics education, pedagogy, quantum mechanics — collegemathteaching @ 9:15 pm

A couple of weeks ago, I attended “Mathfest” in Madison, WI. It was time well spent. The main speaker talked about the connections between algebraic geometry and applied mathematics; there were also good talks about surface approximations and about the applications of topology (even the abstract stuff from algebraic topology).

I just got back from a university conference; there the idea of “interdisciplinary education” came up.

This can be somewhat problematic in mathematics; here is why: I found that one of the toughest things about teaching upper division mathematics to undergraduates is to reshape their intuitions. Here is a quick example: suppose you were told that \int^{\infty}_1 f(x) dx is finite and that, say, f is everywhere non-negative and is continuous. Then lim_{x \rightarrow \infty} f(x) = ? Answer: either zero or it might not exist; in fact, there is no guarantee that f is even bounded!

This, of course, violates the intuition developed in calculus, and it is certainly at odds with the intuition developed in science and engineering courses. Example: just look at the “proofs” that the derivative (or second derivative) operator is Hermitian provided f is square integrable that you find in many quantum mechanics textbooks.

Developing the proper “mathematics attitude” takes time and it doesn’t help if the mathematics student is too immersed in other disciplines…at least it doesn’t help if an intellectually immature math student is getting bad intuition reinforced from other disciplines.

June 5, 2012

Quantum Mechanics, Hermitian Operators and Square Integrable Functions

Filed under: advanced mathematics, analysis, applied mathematics, calculus, improper integrals, integrals, quantum mechanics, science — collegemathteaching @ 8:36 pm

In one dimensional quantum mechanics, the state vectors are taken from the Hilbert space of complex valued “square integrable” functions, and the observables correspond to the so-called “Hermitian operators”. That is, if we let the state vectors be represented by \psi(x) = f(x) + ig(x) and we say \psi \cdot \phi = \int^{\infty}_{-\infty} \overline{\psi} \phi dx where the overline decoration denotes complex conjugation.

The state vectors are said to be “square integrable” which means, strictly speaking, that \int^{\infty}_{-\infty} \overline{\psi}\psi dx is finite.
However, there is another hidden assumption beyond the integral existing and being defined and finite. See if you can spot the assumption in the following remarks:

Suppose we wish to show that the operator \frac{d^2}{dx^2} is Hermitian. To do that we’d have to show that:
\int^{\infty}_{-\infty} \overline{\frac{d^2}{dx^2}\phi} \psi dx = \int^{\infty}_{-\infty} \overline{\phi}\frac{d^2}{dx^2}\psi dx . This doesn’t seem too hard to do at first, if we use integration by parts:
\int^{\infty}_{-\infty} \overline{\frac{d^2}{dx^2}\phi} \psi dx = [\overline{\frac{d}{dx}\phi} \psi]^{\infty}_{-\infty} - \int^{\infty}_{-\infty}\overline{\frac{d}{dx}\phi} \frac{d}{dx}\psi dx . Now because the functions are square integrable, the [\overline{\frac{d}{dx}\phi} \psi]^{\infty}_{-\infty} term is zero (the functions must go to zero as x tends to infinity) and so we have: \int^{\infty}_{-\infty} \overline{\frac{d^2}{dx^2}\phi} \psi dx = - \int^{\infty}_{-\infty}\overline{\frac{d}{dx}\phi} \frac{d}{dx}\psi dx . Now we use integration by parts again:
- \int^{\infty}_{-\infty}\overline{\frac{d}{dx}\phi} \frac{d}{dx}\psi dx = -[\overline{\phi} \frac{d}{dx}\psi]^{\infty}_{-\infty} + \int^{\infty}_{-\infty} \overline{\phi}\frac{d^2}{dx^2} \psi dx which is what we wanted to show.

Now did you catch the “hidden assumption”?

Here it is: it is possible for a function \psi to be square integrable but to be unbounded!

If you wish to work this out for yourself, here is a hint: imagine a rectangle with height 2^{k} and base of width \frac{1}{2^{3k}} . Let f be a function whose graph is a constant function of height 2^{k} for x \in [k - \frac{1}{2^{3k+1}}, k + \frac{1}{2^{3k+1}}] for all positive integers k and zero elsewhere. Then f^2 has height 2^{2k} over all of those intervals which means that the area enclosed by each rectangle (tall, but thin rectangles) is \frac{1}{2^k} . Hence \int^{\infty}_{-\infty} f^2 dx = \frac{1}{2} + \frac{1}{4} + ...\frac{1}{2^k} +.... = \frac{1}{1-\frac{1}{2}} - 1 = 1 . f is certainly square integrable but is unbounded!

It is easy to make f into a continuous function; merely smooth by a bump function whose graph stays in the tall, thin rectangles. Hence f can be made to be as smooth as desired.

So, mathematically speaking, to make these sorts of results work, we must make the assumption that lim_{x \rightarrow \infty} \psi(x) = 0 and add that to the “square integrable” assumption.

May 26, 2012

Eigenvalues, Eigenvectors, Eigenfunctions and all that….

Filed under: advanced mathematics, applications of calculus, applied mathematics, calculus, differential equations, linear albegra, matrix algebra, partial differential equations, physics, quantum mechanics, Uncategorized, vector spaces — collegemathteaching @ 10:35 pm

The purpose of this note is to give a bit of direction to the perplexed student.

I am not going to go into all the possible uses of eigenvalues, eigenvectors, eigenfuntions and the like; I will say that these are essential concepts in areas such as partial differential equations, advanced geometry and quantum mechanics:

Quantum mechanics, in particular, is a specific yet very versatile implementation of this scheme. (And quantum field theory is just a particular example of quantum mechanics, not an entirely new way of thinking.) The states are “wave functions,” and the collection of every possible wave function for some given system is “Hilbert space.” The nice thing about Hilbert space is that it’s a very restrictive set of possibilities (because it’s a vector space, for you experts); once you tell me how big it is (how many dimensions), you’ve specified your Hilbert space completely. This is in stark contrast with classical mechanics, where the space of states can get extraordinarily complicated. And then there is a little machine — “the Hamiltonian” — that tells you how to evolve from one state to another as time passes. Again, there aren’t really that many kinds of Hamiltonians you can have; once you write down a certain list of numbers (the energy eigenvalues, for you pesky experts) you are completely done.

(emphasis mine).

So it is worth understanding the eigenvector/eigenfunction and eigenvalue concept.

First note: “eigen” is German for “self”; one should keep that in mind. That is part of the concept as we will see.

The next note: “eigenfunctions” really are a type of “eigenvector” so if you understand the latter concept at an abstract level, you’ll understand the former one.

The third note: if you are reading this, you are probably already familiar with some famous eigenfunctions! We’ll talk about some examples prior to giving the formal definition. This remark might sound cryptic at first (but hang in there), but remember when you learned \frac{d}{dx} e^{ax} = ae^{ax} ? That is, you learned that the derivative of e^{ax} is a scalar multiple of itself? (emphasis on SELF). So you already know that the function e^{ax} is an eigenfunction of the “operator” \frac{d}{dx} with eigenvalue a because that is the scalar multiple.

The basic concept of eigenvectors (eigenfunctions) and eigenvalues is really no more complicated than that. Let’s do another one from calculus:
the function sin(wx) is an eigenfunction of the operator \frac{d^2}{dx^2} with eigenvalue -w^2 because \frac{d^2}{dx^2} sin(wx) = -w^2sin(wx). That is, the function sin(wx) is a scalar multiple of its second derivative. Can you think of more eigenfunctions for the operator \frac{d^2}{dx^2} ?

Answer: cos(wx) and e^{ax} are two others, if we only allow for non zero eigenvalues (scalar multiples).

So hopefully you are seeing the basic idea: we have a collection of objects called vectors (can be traditional vectors or abstract ones such as differentiable functions) and an operator (linear transformation) that acts on these objects to yield a new object. In our example, the vectors were differentiable functions, and the operators were the derivative operators (the thing that “takes the derivative of” the function). An eigenvector (eigenfunction)-eigenvalue pair for that operator is a vector (function) that is transformed to a scalar multiple of itself by the operator; e. g., the derivative operator takes e^{ax} to ae^{ax} which is a scalar multiple of the original function.

Formal Definition
We will give the abstract, formal definition. Then we will follow it with some examples and hints on how to calculate.

First we need the setting. We start with a set of objects called “vectors” and “scalars”; the usual rules of arithmetic (addition, multiplication, subtraction, division, distributive property) hold for the scalars and there is a type of addition for the vectors and scalars and the vectors “work together” in the intuitive way. Example: in the set of, say, differentiable functions, the scalars will be real numbers and we have rules such as a (f + g) =af + ag , etc. We could also use things like real numbers for scalars, and say, three dimensional vectors such as [a, b, c] More formally, we start with a vector space (sometimes called a linear space) which is defined as a set of vectors and scalars which obey the vector space axioms.

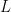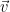Now, we need a linear transformation, which is sometimes called a linear operator. A linear transformation (or operator) is a function L that obeys the following laws: L(\vec{v} + \vec{w}) = L(\vec{v}) + L(\vec{w} ) and L(a\vec{v}) = aL(\vec{v}) . Note that I am using \vec{v} to denote the vectors and the undecorated variable to denote the scalars. Also note that this linear transformation 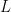L might take one vector space to a different vector space.

Common linear transformations (and there are many others!) and their eigenvectors and eigenvalues.
Consider the vector space of two-dimensional vectors with real numbers as scalars. We can create a linear transformation by matrix multiplication:

L([x,y]^T) = \left[ \begin{array}{cc} a & b \\ c & d \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} ax+ by \\ cx+dy \end{array} \right] (note: [x,y]^T is the transpose of the row vector; we need to use a column vector for the usual rules of matrix multiplication to apply).

It is easy to check that the operation of matrix multiplying a vector on the left by an appropriate matrix is yields a linear transformation.
Here is a concrete example: L([x,y]^T) = \left[ \begin{array}{cc} 1 & 2 \\ 0 & 3 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} x+ 2y \\ 3y \end{array} \right]

So, does this linear transformation HAVE non-zero eigenvectors and eigenvalues? (not every one does).
Let’s see if we can find the eigenvectors and eigenvalues, provided they exist at all.

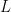For [x,y]^T to be an eigenvector for L , remember that L([x,y]^T) = \lambda [x,y]^T for some real number \lambda

So, using the matrix we get: L([x,y]^T) = \left[ \begin{array}{cc} 1 & 2 \\ 0 & 3 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right]= \lambda \left[ \begin{array}{c} x \\ y \end{array} \right] . So doing some algebra (subtracting the vector on the right hand side from both sides) we obtain \left[ \begin{array}{cc} 1 & 2 \\ 0 & 3 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] - \lambda \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]

At this point it is tempting to try to use a distributive law to factor out \left[ \begin{array}{c} x \\ y \end{array} \right] from the left side. But, while the expression makes sense prior to factoring, it wouldn’t AFTER factoring as we’d be subtracting a scalar number from a 2 by 2 matrix! But there is a way out of this: one can then insert the 2 x 2 identity matrix to the left of the second term of the left hand side:
\left[ \begin{array}{cc} 1 & 2 \\ 0 & 3 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] - \lambda\left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]

Notice that by doing this, we haven’t changed anything except now we can factor out that vector; this would leave:
(\left[ \begin{array}{cc} 1 & 2 \\ 0 & 3 \end{array} \right] - \lambda\left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right] )\left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]

Which leads to:

(\left[ \begin{array}{cc} 1-\lambda & 2 \\ 0 & 3-\lambda \end{array} \right] ) \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right]

Now we use a fact from linear algebra: if [x,y]^T is not the zero vector, we have a non-zero matrix times a non-zero vector yielding the zero vector. This means that the matrix is singular. In linear algebra class, you learn that singular matrices have determinant equal to zero. This means that (1-\lambda)(3-\lambda) = 0 which means that \lambda = 1, \lambda = 3 are the respective eigenvalues. Note: when we do this procedure with any 2 by 2 matrix, we always end up with a quadratic with \lambda as the variable; if this quadratic has real roots then the linear transformation (or matrix) has real eigenvalues. If it doesn’t have real roots, the linear transformation (or matrix) doesn’t have non-zero real eigenvalues.

Now to find the associated eigenvectors: if we start with \lambda = 1 we get
(\left[ \begin{array}{cc} 0 & 2 \\ 0 & 2 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] which has solution \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] . So that is the eigenvector associated with eigenvalue 1.
If we next try \lambda = 3 we get
(\left[ \begin{array}{cc} -2 & 2 \\ 0 & 0 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] which has solution \left[ \begin{array}{c} x \\ y \end{array} \right] = \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] . So that is the eigenvector associated with the eigenvalue 3.

In the general “k-dimensional vector space” case, the recipe for finding the eigenvectors and eigenvalues is the same.
1. Find the matrix 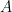A for the linear transformation.
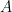2. Form the matrix A - \lambda I which is the same as matrix A except that you have subtracted \lambda from each diagonal entry.
3. Note that det(A - \lambda I) is a polynomial in variable \lambda ; find its roots \lambda_1, \lambda_2, ...\lambda_n . These will be the eigenvalues.
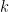4. Start with \lambda = \lambda_1 Substitute this into the matrix-vector equation det(A - \lambda I) \vec{v_1} = \vec{0} and solve for \vec({v_1} . That will be the eigenvector associated with the first eigenvalue. Do this for each eigenvalue, one at a time. Note: you can get up to k “linearly independent” eigenvectors in this manner; that will be all of them.

Practical note
Yes, this should work “in theory” but practically speaking, there are many challenges. For one: for equations of degree 5 or higher, it is known that there is no formula that will find the roots for every equation of that degree (Galios proved this; this is a good reason to take an abstract algebra course!). Hence one must use a numerical method of some sort. Also, calculation of the determinant involves many round-off error-inducing calculations; hence sometimes one must use sophisticated numerical techniques to get the eigenvalues (a good reason to take a numerical analysis course!)

Consider a calculus/differential equation related case of eigenvectors (eigenfunctions) and eigenvalues.
Our vectors will be, say, infinitely differentiable functions and our scalars will be real numbers. We will define the operator (linear transformation) D^n = \frac{d^n}{dx^n} , that is, the process that takes the n’th derivative of a function. You learned that the sum of the derivatives is the derivative of the sums and that you can pull out a constant when you differentiate. Hence D^n is a linear operator (transformation); we use the term “operator” when we talk about the vector space of functions, but it is really just a type of linear transformation.

We can also use these operators to form new operators; that is (D^2 + 3D)(y) = D^2(y) + 3D(y) = \frac{d^2y}{dx^2} + 3\frac{dy}{dx} We see that such “linear combinations” of linear operators is a linear operator.

So, what does it mean to find eigenvectors and eigenvalues of such beasts?

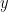Suppose we with to find the eigenvectors and eigenvalues of (D^2 + 3D) . An eigenvector is a twice differentiable function y (ok, we said “infinitely differentiable”) such that (D^2 + 3D) = \lambda y or \frac{d^2y}{dx^2} + 3\frac{dy}{dx} = \lambda y which means \frac{d^2y}{dx^2} + 3\frac{dy}{dx} - \lambda y = 0 . You might recognize this from your differential equations class; the only “tweak” is that we don’t know what \lambda is. But if you had a differential equations class, you’d recognize that the solution to this differential equation depends on the roots of the characteristic equation m^2 + 3m - \lambda = 0 which has solutions: m = -\frac{3}{2} \pm \frac{\sqrt{9-4\lambda}}{2} and the solution takes the form e^{m_1}, e^{m_2} if the roots are real and distinct, e^{ax}sin(bx), e^{ax}cos(bx) if the roots are complex conjugates a \pm bi and e^{m}, xe^{m} if there is a real, repeated root. In any event, those functions are the eigenfunctions and these very much depend on the eigenvalues.

Of course, reading this little note won’t make you an expert, but it should get you started on studying.

I’ll close with a link on how these eigenfunctions and eigenvalues are calculated (in the context of solving a partial differential equation).

August 19, 2011

Quantum Mechanics and Undergraduate Mathematics XV: sample problem for stationary states

Filed under: advanced mathematics, applied mathematics, partial differential equations, physics, quantum mechanics — collegemathteaching @ 7:24 pm

I feel a bit guilty as I haven’t gone over an example of how one might work out a problem. So here goes:

Suppose our potential function is some sort of energy well: V(x) = 0 for 0 < x < 1 and V(x) = \infty elsewhere.
Note: I am too lazy to keep writing \hbar so I am going with h for now.

So, we have the two Schrödinger equations with \psi being the state vector and \eta_k being one of the stationary states:
-\frac{h^2}{2m} \frac{\partial}{\partial x^2}\eta_k + V(x) \eta_k = ih\frac{\partial}{\partial t} \eta_k
-\frac{h^2}{2m} \frac{\partial}{\partial x^2}\eta_k + V(x) \eta_k = e_k \eta_k

Where e_k are the eigenvalues for \eta_k

Now apply the potential for 0 < x < 1 and the equations become:
-\frac{h^2}{2m} \frac{\partial}{\partial x^2}\eta_k = ih\frac{\partial}{\partial t} \eta_k
-\frac{h^2}{2m} \frac{\partial}{\partial x^2}\eta_k = e_k \eta_k

Yes, I know that equation II is a consequence of equation I.

Now we use a fact from partial differential equations: the first equation is really a form of the “diffusion” or “heat” equation; it has been shown that once one takes boundary conditions into account, the equation posses a unique solution. Hence if we find a solution by any means necessary, we don’t have to worry about other solutions being out there.

So attempt a solution of the form \eta_k = X_k T_k where the first factor is a function of x alone and the second is of t alone.
Now put into the second equation:

-\frac{h^2}{2m} X^{\prime\prime}_kT_k = e_k XT

Now assume T \ne 0 and divide both sides by T and do a little algebra to obtain:
X^{\prime\prime}_k +\frac{2m e_k}{h^2}X_k = 0
e_k are the eigenvalues for the stationary states; assume that these are positive and we obtain:
X = a_k cos(\frac{\sqrt{2m e_k}}{h} x) + b_k sin(\frac{\sqrt{2m e_k}}{h} x)
from our knowledge of elementary differential equations.
Now for x = 0 we have X_k(0) = a_k . Our particle is in our well and we can’t have values below 0; hence a_k = 0 . Now X(x) = b_k sin(\frac{\sqrt{2m e_k}}{h} x)
We want zero at x = 1 so \frac{\sqrt{2m e_k}}{h} = k\pi which means e_k = \frac{(k \pi h)^2}{2m} .

Now let’s look at the first Schrödinger equation:
-\frac{h^2}{2m}X_k^{\prime\prime} T_k = ihT_k^{\prime}X_k
This gives the equation: \frac{X_k^{\prime\prime}}{X_k} = -\frac{ 2m i}{h} \frac{T_k^{\prime}}{T_k}
Note: in partial differential equations, it is customary to note that the left side of the equation is a function of x alone and therefore independent of t and that the right hand side is a function of T alone and therefore independent of x ; since these sides are equal they must be independent of both t and x and therefore constant. But in our case, we already know that \frac{X_k^{\prime\prime}}{X_k} = -2m\frac{e_k}{h^2} . So our equation involving T becomes \frac{T_k^{\prime}}{T_k} = -2m\frac{e_k}{h^2} i \frac{h}{2m} = i\frac{e_k}{h} so our differential equation becomes
T_k {\prime} = i \frac{e_k}{h} T_k which has the solution T_k = c_k exp(i \frac{e_k}{h} t)

So our solution is \eta_k = d_k sin(\frac{\sqrt{2m e_k}}{h} x) exp(i \frac{e_k}{h} t) where e_k = \frac{(k \pi h)^2}{2m} .

This becomes \eta_k = d_k sin(k\pi x) exp(i (k \pi)^2 \frac{\hbar}{2m} t) which, written in rectangular complex coordinates is d_k sin(k\pi x) (cos((k \pi)^2 \frac{\hbar}{2m} t) + i sin((k \pi)^2 \frac{\hbar}{2m} t)

Here are some graphs: we use m = \frac{\hbar}{2} and plot for k = 1, k = 3 and t \in {0, .1, .2, .5} . The plot is of the real part of the stationary state vector.

August 17, 2011

Quantum Mechanics and Undergraduate Mathematics XIV: bras, kets and all that (Dirac notation)

Filed under: advanced mathematics, applied mathematics, linear albegra, physics, quantum mechanics, science — collegemathteaching @ 11:29 pm

Up to now, I’ve used mathematical notation for state vectors, inner products and operators. However, physicists use something called “Dirac” notation (“bras” and “kets”) which we will now discuss.

Recall: our vectors are integrable functions \psi: R^1 \rightarrow C^1 where \int^{-\infty}_{\infty} \overline{\psi} \psi dx converges.

Our inner product is: \langle \phi, \psi \rangle = \int^{-\infty}_{\infty} \overline{\phi} \psi dx

Here is the Dirac notation version of this:
A “ket” can be thought of as the vector \langle , \psi \rangle . Of course, there is an easy vector space isomorphism (Hilbert space isomorphism really) between the vector space of state vectors and kets given by \Theta_k \psi = \langle,\psi \rangle . The kets are denoted by |\psi \rangle .
Similarly there are the “bra” vectors which are “dual” to the “kets”; these are denoted by \langle \phi | and the vector space isomorphism is given by \Theta_b \psi = \langle,\overline{\psi} | . I chose this isomorphism because in the bra vector space, a \langle\alpha,| = \langle \overline{a} \alpha,| . Then there is a vector space isomorphism between the bras and the kets given by \langle \psi | \rightarrow |\overline{\psi} \rangle .

Now \langle \psi | \phi \rangle is the inner product; that is \langle \psi | \phi \rangle = \int^{\infty}_{-\infty} \overline{\psi}\phi dx

By convention: if A is a linear operator, \langle \psi,|A = \langle A(\psi)| and A |\psi \rangle = |A(\psi) \rangle Now if A is a Hermitian operator (the ones that correspond to observables are), then there is no ambiguity in writing \langle \psi | A | \phi \rangle .

This leads to the following: let A be an operator corresponding to an observable with eigenvectors \alpha_i and eigenvalues a_i . Let \psi be a state vector.
Then \psi = \sum_i \langle \alpha_i|\psi \rangle \alpha_i and if Y is a random variable corresponding to the observed value of A , then P(Y = a_k) = |\langle \alpha_k | \psi \rangle |^2 and the expectation E(A) = \langle \psi | A | \psi \rangle .

August 11, 2011

Quantum Mechanics and Undergraduate Mathematics XIII: simplifications and wave-particle duality

Filed under: advanced mathematics, differential equations, distributions, generalized functions, physics, quantum mechanics, science — collegemathteaching @ 3:14 pm

In an effort to make the subject a bit more accessible to undergraduate mathematics students who haven’t had much physics training, we’ve made some simplifications. We’ve dealt with the “one dimensional, non-relativistic situation” which is fine. But we’ve also limited ourselves to the case where:
1. state vectors are actual functions (like those we learn about in calculus)
2. eigenvalues are discretely distributed (e. g., the set of eigenvalues have no limit points in the usual topology of the real line)
3. each eigenvalue corresponds to a unique eigenvector.

In this post we will see what trouble simplifications 1 and 2 cause and why they cannot be lived with. Hey, quantum mechanics is hard!

Finding Eigenvectors for the Position Operator
Let X denote the “position” operator and let us seek out the eigenvectors for this operator.
So X\delta = x_0 \delta where \delta is the eigenvector and x_0 is the associated eigenvalue.
This means x\delta = x_0\delta which implies (x-x_0)\delta = 0 .
This means that for x \neq x_0, \delta = 0 and \delta can be anything for x = x_0 . This would appear to allow the eigenvector to be the “everywhere zero except for x_0 ” function. So let \delta be such a function. But then if \psi is any state vector, \int_{-\infty}^{\infty} \overline{\delta}\psi dx = 0 and \int_{-\infty}^{\infty} \overline{\delta}\delta dx = 0 . Clearly this is unacceptable; we need (at least up to a constant multiple) for \int_{-\infty}^{\infty} \overline{\delta}\delta dx = 1

The problem is that restricting our eigenvectors to the class of functions is just too restrictive to give us results; we have to broaden the class of eigenvectors. One way to do that is to allow for distributions to be eigenvectors; the distribution we need here is the dirac delta. In the reference I linked to, one can see how the dirac delta can be thought of as a sort of limit of valid probability density functions. Note: \overline{\delta} = \delta .

So if we let \delta_0 denote the dirac that is zero except for x = x_0 , we recall that \int_{\infty}^{\infty} \delta_0 \psi dx = \psi(x_0) . This means that the probability density function associated with the position operator is P(X = x_0) = |\psi(x_0)|^2

This has an interesting consequence: if we measure the particle’s position at x = x_0 then the state vector becomes \delta_0 . So the new density function based on an immediate measurement of position would be P( X = x_0) = |\langle \delta_0, \delta_0 \rangle|^2 = 1 and P(X = x) = 0 elsewhere. The particle behaves like a particle with a definite “point” position.

Momentum: a different sort of problem

At first the momentum operator P\psi = -i \hbar \frac{d\psi}{dx} seems less problematic. Finding the eigenvectors and eigenfunctions is a breeze: if \theta_0 is the eigenvector with eigenvalue p_0 then:
\frac{d}{dx} \theta_0 = \frac{i}{\hbar}p_0\theta_0 has solution \theta_0 = exp(i p_0 \frac{x}{\hbar}) .
Do you see the problem?

There are a couple of them: first, this provides no restriction on the eigenvalues; in fact the eigenvalues can be any real number. This violates simplification number 2. Secondly, |\theta_0|^2 = 1 therefore |\langle \theta_0, \theta_0 \rangle |^2 = \infty . Our function is far from square integrable and therefore not a valid “state vector” in its present form. This is where the famous “normalization” comes into play.

Mathematically, one way to do this is to restrict the domain (say, limit the non-zero part to x_0 < x < x_1 ) and multiply by an appropriate constant.

Getting back to our state vector: exp(ip_0 \frac{x}{\hbar}) = cos(\frac{p_0 x}{\hbar}) + i sin(\frac{p_0 x}{\hbar}) . So if we measure momentum, we have basically given a particle a wave characteristic with wavelength \frac{\hbar}{p_0} .

Now what about the duality? Suppose we start by measuring a particle’s position thereby putting the state vector in to \psi = \delta_0 . Now what would be the expectation of momentum? We know that the formula is E(P) = -i\hbar \int-{-\infty}^{infty} \delta_0 \frac{\partial \delta_0}{\partial x} dx . But this quantity is undefined because \frac{\partial \delta_0}{\partial x} is undefined.

If we start in a momentum eigenvector and then wish to calculate the position density function (the expectation will be undefined), we see that |\theta_0|^2 = 1 which can be interpreted to mean that any position measurement is equally likely.

Clearly, momentum and position are not compatible operators. So let’s calculate XP - PX
XP \phi = x(-i\hbar \frac{d}{dx} \phi) = -xi\hbar \frac{d}{dx} \phi and PX\phi = -i \hbar\frac{d}{dx} (x \phi) = -i \hbar (\phi + x \frac{d}{dx}\phi) hence (XP - PX)\phi = i\hbar \phi . Therefore XP-PX = i\hbar . Therefore our generalized uncertainty relation tells us \Delta X \Delta P \geq \frac{1}{2}h
(yes, one might object that \Delta X really shouldn’t be defined….) but this uncertainty relation does hold up. So if one uncertainty is zero, then the other must be infinite; exact position means no defined momentum and vice versa.

So: exact, pointlike position means no defined momentum is possible (hence no wave like behavior) but an exact momentum (pure wave) means no exact pointlike position is possible. Also, remember that measurement of position endows a point like state vector of \delta_0 which destroys the wave like property; measurement of momentum endows a wave like state vector \theta_0 and therefore destroys any point like behavior (any location is equally likely to be observed).

Quantum Mechanics and Undergraduate Mathematics XII: position and momentum operators

Filed under: advanced mathematics, applied mathematics, physics, probability, quantum mechanics, science — collegemathteaching @ 1:52 am

Recall that the position operator is X \psi = x\psi and the momentum operator P \psi = -i\hbar \frac{d}{dx} \psi .

Recalling our abuse of notation that said that the expected value E = \langle \psi, A \psi \rangle , we find that the expected value of position is E(X) = \int_{-\infty}^{\infty} x |\psi|^2 dx . Note: since \int_{-\infty}^{\infty} |\psi|^2 dx = 1, we can view |\psi|^2 as a probability density function; hence if f is any “reasonable” function of x , then E(f(X)) = \int_{-\infty}^{\infty} f(x) |\psi|^2 dx . Of course we can calculate the variance and other probability moments in a similar way; e. g. E(X^2) = \int_{-\infty}^{\infty} x |\psi|^2 dx .

Now we turn to momentum; E(P) = \langle \psi, -i\hbar \frac{d}{dx} \psi \rangle = \int_{-\infty}^{\infty} \overline{\psi}\frac{d}{dx}\psi dx and E(P^2) = \langle \psi, P^2\psi \rangle = \langle P\psi, P\psi \rangle = \int_{-\infty}^{\infty} |\frac{d}{dx}\psi|^2 dx

So, back to position: we can now use the fact that |\psi|^2 is a valid density function associated with finding the expected value of position and call this the position probability density function. Hence P(x_1 < x < x_2) = \int_{-\infty}^{\infty} |\psi|^2 dx . But we saw that this can change with time so: P(x_1 < x < x_2; t) = \int_{-\infty}^{\infty} |\psi(x,t)|^2 dx

This is a great chance to practice putting together: differentiation under the integral sign, Schrödinger’s equation and integration by parts. I recommend that the reader try to show:

\frac{d}{dt} \int_{x_1}^{x_2} \overline{\psi}\psi dx = \frac{ih}{2m}(\overline{\psi}\frac{d \psi}{dx}-\psi \frac{d \overline{\psi}}{dx})_{x_1}^{x_2}

The details for the above calculation (students: try this yourself first! 🙂 )

Differentiation under the integral sign:
\frac{d}{dt} \int_{x_1}^{x_2} \overline{\psi} \psi dx = \int_{x_1}^{x_2}\overline{\psi} \frac{\partial \psi}{\partial t} + \psi \frac{\partial \overline{ \psi}}{\partial t} dt

Schrödinger’s equation (time dependent version) with a little bit of algebra:
\frac{\partial \psi}{\partial t} = \frac{i \hbar}{2m} \frac{\partial^2 \psi}{\partial x^2} - \frac{i}{\hbar}V \psi
\frac{\partial \overline{\psi}}{\partial t} = \frac{i \hbar}{2m} \frac{\partial^2 \overline{\psi}}{\partial x^2} + \frac{i}{\hbar}V \overline{\psi}

Note: V is real.

Algebra: eliminate the partial with respect to time terms; multiply the top equation by \overline{\psi} and the second by \psi . Then add the two to obtain:
\overline{\psi} \frac{\partial \psi}{\partial t} + \psi \frac{\partial \overline{ \psi}}{\partial t} = \frac{i \hbar}{2m}(\overline{\psi} \frac{\partial^2 \psi}{\partial x^2} + \psi \frac{\partial^2 \overline{ \psi}}{\partial x^2})

Now integrate by parts:
\frac{i \hbar}{2m} \int_{x_2}^{x_1} (\overline{\psi} \frac{\partial^2 \psi}{\partial x^2} + \psi \frac{\partial^2 \overline{ \psi}}{\partial x^2}) dx =

\frac{ih}{2m} ((\overline{\psi} \frac{\partial \psi}{\partial x})_{x_1}^{x_2} - \int_{x_2}^{x_1} \frac{\partial \overline{\psi}}{\partial x} \frac{\partial \psi}{\partial x} - ( (\psi \frac{\partial \overline{\psi}}{\partial x})_{x_1}^{x_2} - \int_{x_2}^{x_1}\frac{\partial \psi}{\partial x}\frac{\partial \overline{\psi}}{\partial x}dx)

Now the integrals cancel each other and we obtain our result.

It is common to denote -\frac{ih}{2m}(\overline{\psi}\frac{d \psi}{dx}-\psi \frac{d \overline{\psi}}{dx} by S(x,t) (note the minus sign) and to say \frac{d}{dt}P(x_1 < x < x_2 ; t) = S(x_1,t) - S(x_2,t) (see the reason for the minus sign?)

S(x,t) is called the position probability current at the point x at time t One can think of this as a "probability flow rate" over the point x at time t ; the quantity S(x_1, t) - S(x_2, t) will tell you if the probability of finding the particle between position x_1 and x_2 is going up (positive sign) or down, and by what rate. But it is important that these are position PROBABILITY current and not PARTICLE current; same for |\psi |^2 ; this is the position probability density function, not the particle density function.

NOTE I haven’t talked about the position and momentum eigenvalues or eigenfuctions. We’ll do that in our next post; we’ll run into some mathematical trouble here. No, it won’t be with the position because we already know what a distribution is; the problem is that we’ll find the momentum eigenvector really isn’t square integrable….or even close.

August 10, 2011

Quantum Mechanics and Undergraduate Mathematics XI: an example (potential operator)

Filed under: advanced mathematics, calculus, differential equations, quantum mechanics, science — collegemathteaching @ 8:41 pm

Recall the Schrödinger equations:
-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \eta_k + V(x) \eta_k = e_k \eta_k and
-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} \phi + V(x) \phi = i\hbar \frac{\partial}{\partial t}\phi

The first is the time-independent equation which uses the eigenfuctions for the energy operator (Hamiltonian) and the second is the time-dependent state vector equation.

Now suppose that we have a specific energy potential V(x) ; say V(x) = \frac{1}{2}kx^2 . Note: in classical mechanics this follows from Hooke’s law: F(x) = -kx = -\frac{dV}{dx} . In classical mechanics this leads to the following differential equation: ma = m \frac{d^2x}{dt^2} = -kx which leads to \frac{d^2x}{dt^2} + (\frac{k}{m})x = 0 which has general solution x = C_1 sin(wt) +C_2cos(wt) where w = \sqrt{\frac{k}{m}} The energy of the system is given by E = \frac{1}{2}mw^2A^2 where A is the maximum value of x which, of course, is determined by the initial conditions (velocity and displacement at t = 0 ).

Note that there are no a priori restrictions on A . Notation note: A stands for a real number here, not an operator as it has previously.

So what happens in the quantum world? We can look at the stationary states associated with this operator; that means turning to the first Schrödinger equation and substituting V(x) = \frac{1}{2}kx^2 (note k > 0 ):

-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} \eta_k + \frac{1}{2}kx^2\eta_k = e_k \eta_k

Now let’s do a little algebra to make things easier to see: divide by the leading coefficient and move the right hand side of the equation to the left side to obtain:

\frac{d^2}{dx^2} \eta_k + (\frac{2 e_k m}{(\hbar)^2} - \frac{km}{(\hbar)^2}x^2) \eta_k = 0

Now let’s do a change of variable: let x = rz Now we can use the chain rule to calculate: \frac{d^2}{dx^2} = \frac{1}{r^2}\frac{d^2}{dz^2} . Substitution into our equation in x and multiplication on both sides by r^2 yields:
\frac{d^2}{dz^2} \eta_k + (r^2 \frac{2 e_k m}{\hbar^2} - r^4\frac{km}{(\hbar)^2}z^2) \eta_k = 0
Since r is just a real valued constant, we can choose r = (\frac{km}{\hbar^2})^{-1/4} .
This means that r^2 \frac{2 e_k m}{\hbar^2} = \sqrt{\frac{\hbar^2}{km}}\frac{2 e_k m}{(\hbar)^2} = 2 \frac{e_k}{\hbar}\sqrt{\frac{m}{k}}

So our differential equation has been transformed to:
\frac{d^2}{dz^2} \eta_k + (2 \frac{e_k}{\hbar}\sqrt{\frac{m}{k}} - z^2) \eta_k = 0

We are now going to attempt to solve the eigenvalue problem, which means that we will seek values for e_k that yield solutions to this differential equation; a solution to the differential equation with a set eigenvalue will be an eigenvector.

If we were starting from scratch, this would require quite a bit of effort. But since we have some ready made functions in our toolbox, we note 🙂 that setting e_k = (2k+1) \frac{\hbar}{2} \sqrt{{k}{m}} gives us:
\frac{d^2}{dz^2} \eta_k + (2K+1 - z^2) \eta_k = 0

This is the famous Hermite differential equation.

One can use techniques of ordinary differential equations (say, series techniques) to solve this for various values of n .
It turns out that the solutions are:

\eta_k = (-1)^k (2^k k! \sqrt{\pi})^{-1/2} exp(\frac{z^2}{2})\frac{d^k}{dz^k}exp(-z^2) = (2^k k! \sqrt{\pi})^{-1/2} exp(-z^/2)H_k(z) where here H_k(z) is the k'th Hermite polynomial. Here are a few of these:

Graphs of the eigenvectors (in z ) are here:

(graphs from here)

Of importance is the fact that the allowed eigenvalues are all that can be observed by a measurement and that these form a discrete set.

Ok, what about other operators? We will study both the position and the momentum operators, but these deserve their own post as this is where the fun begins! 🙂

Older Posts »

Blog at WordPress.com.