Just a reminder: if  is a series and
is a series and  is some sequence consisting of 0’s and 1’s then a selective sum of the series is
is some sequence consisting of 0’s and 1’s then a selective sum of the series is  . The selective sum concept is discussed in the MAA book Real Infinite Series (MAA Textbooks) by Bonar and Khoury (2006) and I was introduced to the concept by Ferdinands’s article Selective Sums of an Infinite Series in the June 2015 edition of Mathematics Magazine (Vol. 88, 179-185).
. The selective sum concept is discussed in the MAA book Real Infinite Series (MAA Textbooks) by Bonar and Khoury (2006) and I was introduced to the concept by Ferdinands’s article Selective Sums of an Infinite Series in the June 2015 edition of Mathematics Magazine (Vol. 88, 179-185).
There is much of interest there, especially if one considers convergent series or alternating series.
This post will be about divergent series of positive terms for which  and
and  for all
for all 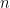 .
.
The first fun result is this one: any selected 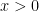 is a selective sum of such a series. The proof of this isn’t that bad. Since
is a selective sum of such a series. The proof of this isn’t that bad. Since  we can find a smallest
we can find a smallest 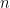 such that
such that  . Clearly if
. Clearly if  we are done: our selective sum has
we are done: our selective sum has  and the rest of the
and the rest of the  .
.
If not, set  and note that because the series diverges, there is a largest
and note that because the series diverges, there is a largest  so that
so that  . Now if
. Now if  we are done, else let
we are done, else let  and note
and note  . Now because the
. Now because the  tend to zero, there is some first
tend to zero, there is some first  so that
so that  . If this is equality then the required sum is
. If this is equality then the required sum is  , else we can find the largest
, else we can find the largest  so that
so that 
This procedure can be continued indefinitely. So if we label  we see that
we see that  form an increasing, bounded sequence which converges to the least upper bound of its range, and it isn’t hard to see that the least upper bound is
form an increasing, bounded sequence which converges to the least upper bound of its range, and it isn’t hard to see that the least upper bound is  because
because 
So now that we can obtain any positive real number as the selective sum of such a series, what can we say about the set of all selective sums for which almost all of the  (that is, all but a finite number of the
(that is, all but a finite number of the  are zero).
are zero).
Answer: the set of all such selective sums are dense in the real line, and this isn’t that hard to see, given our above construction. Let 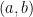 be any open interval in the real line and let
be any open interval in the real line and let  . Then one can find some
. Then one can find some 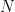 such that for all
such that for all  we have
we have  . Now consider our construction and choose
. Now consider our construction and choose 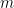 large enough such that
large enough such that  . Then the
. Then the  represents the finite selected sum that lies in the interval
represents the finite selected sum that lies in the interval 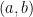 .
.
We can be even more specific if we now look at a specific series, such as the harmonic series  . We know that the set of finite selected sums forms a dense subset of the real line. But it turns out that the set of select sums is the rationals. I’ll give a slightly different proof than one finds in Bonar and Khoury.
. We know that the set of finite selected sums forms a dense subset of the real line. But it turns out that the set of select sums is the rationals. I’ll give a slightly different proof than one finds in Bonar and Khoury.
First we prove that every rational in ![(0,1]](https://s0.wp.com/latex.php?latex=%280%2C1%5D+&bg=ffffff&fg=000000&s=0&c=20201002) is a finite select sum. Clearly 1 is a finite select sum. Otherwise: Given
is a finite select sum. Clearly 1 is a finite select sum. Otherwise: Given  we can find the minimum
we can find the minimum 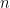 so that
so that  . If
. If  we are done. Otherwise: the strict inequality shows that
we are done. Otherwise: the strict inequality shows that  which means
which means  . Then note
. Then note  and this fraction has a strictly smaller numerator than
and this fraction has a strictly smaller numerator than 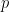 . So we can repeat our process with this new rational number. And this process must eventually terminate because the numerators generated from this process form a strictly decreasing sequence of positive integers. The process can only terminate when the new faction has a numerator of 1. Hence the original fraction is some sum of fractions with numerator 1.
. So we can repeat our process with this new rational number. And this process must eventually terminate because the numerators generated from this process form a strictly decreasing sequence of positive integers. The process can only terminate when the new faction has a numerator of 1. Hence the original fraction is some sum of fractions with numerator 1.
Now if the rational number  in question is greater than one, one finds
in question is greater than one, one finds  so that
so that  but
but  . Then write
. Then write  and note that its magnitude is less than
and note that its magnitude is less than  . We then use the procedure for numbers in
. We then use the procedure for numbers in  noting that our starting point excludes the previously used terms of the harmonic series.
noting that our starting point excludes the previously used terms of the harmonic series.
There is more we can do, but I’ll stop here for now.
for now) and a subspace is defined to be a set of vectors that is closed under both vector addition and scalar multiplication. Here are a couple of examples of non-subspaces:
. Now this space IS closed under scalar multiplication, note that this space IS closed under additive inverses. But it is not closed under addition as
for
.
are closed under vector addition but not under scalar multiplication.


