Reminder: this series is NOT for the student who is attempting to learn calculus for the first time.
Derivatives This is dealing with differentiable functions  and no, I will NOT be talking about maps between tangent bundles. Yes, my differential geometry and differential topology courses were on the order of 30 years ago or so. 🙂
and no, I will NOT be talking about maps between tangent bundles. Yes, my differential geometry and differential topology courses were on the order of 30 years ago or so. 🙂
In calculus 1, we typically use the following definitions for the derivative of a function at a point:  . This is opposed to the derivative function which can be thought of as the one dimensional gradient of
. This is opposed to the derivative function which can be thought of as the one dimensional gradient of 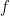 .
.
The first definition is easier to use for some calculations, say, calculating the derivative of  at a point. (hint, if you need one: use
at a point. (hint, if you need one: use  then it is easier to factor). It can be used for proving a special case of the chain rule as well (the case there we are evaluating
then it is easier to factor). It can be used for proving a special case of the chain rule as well (the case there we are evaluating 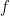 at
at  and
and  for at most a finite number of points near
for at most a finite number of points near  .)
.)
When introducing this concept, the binomial expansion theorem is very handy to use for many of the calculations.
Now there is another definition for the derivative that is helpful when proving the chain rule (sans restrictions).
Note that as  we have
we have  . We can now view
. We can now view  as a function of
as a function of 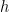 which goes to zero as
which goes to zero as 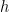 does.
does.
That is,  where
where  and
and  is the best linear approximation for
is the best linear approximation for 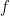 at
at  .
.
We’ll talk about the chain rule a bit later.
But what about the derivative and examples?
It is common to develop intuition for the derivative as applied to nice, smooth..ok, analytic functions. And this might be a fine thing to do for beginning calculus students. But future math majors might benefit from being exposed to just a bit more so I’ll give some examples.
Now, of course, being differentiable at a point means being continuous there (the limit of the numerator of the difference quotient must go to zero for the derivative to exist). And we all know examples of a function being continuous at a point but not being differentiable there. Examples:  are all continuous at zero but none are differentiable there; these give examples of a corner, vertical tangent and a cusp respectively.
are all continuous at zero but none are differentiable there; these give examples of a corner, vertical tangent and a cusp respectively.
But for many of the piecewise defined examples, say,  for
for  and
and  for
for 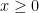 the derivative fails to exist because the respective derivative functions fail to be continuous at
the derivative fails to exist because the respective derivative functions fail to be continuous at  ; the same is true of the other stated examples.
; the same is true of the other stated examples.
And of course, we can show that  has
has 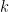 continuous derivatives at the origin but not
continuous derivatives at the origin but not  derivatives.
derivatives.
But what about a function with a discontinuous derivative? Try  for
for  and zero at
and zero at  . It is easy to see that the derivative exists for all
. It is easy to see that the derivative exists for all  but the first derivative fails to be continuous at the origin.
but the first derivative fails to be continuous at the origin.
The derivative is 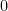 at
at 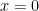 and
and  for
for  which is not continuous at the origin.
which is not continuous at the origin.
Ok, what about a function that is differentiable at a single point only? There are different constructions, but if  for
for  rational,
rational,  for
for  irrational is both continuous and, yes, differentiable at
irrational is both continuous and, yes, differentiable at 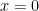 (nice application of the Squeeze Theorem on the difference quotient).
(nice application of the Squeeze Theorem on the difference quotient).
Yes, there are everywhere continuous, nowhere differentiable functions.
so the integral is transformed into
and so we’ve entered the realm of rational functions. Ok, ok, there is some work to do.
be such that
then:
gets transformed:
and then
and the integral becomes
which is a rational function integral.








