Projections, regressions and Anscombe’s quartet…

Data and its role in journalism is a hot topic among some of the bloggers that I regularly follow. See: Nate Silver on what he hopes to accomplish with his new website, and Paul Krugman’s caveats on this project. The debate is, as I see it, about the role of data and the role of having expertise in a subject when it comes to providing the public with an accurate picture of what is going on.

Then I saw this meme on a Facebook page:

These two things (the discussion and meme) lead me to make this post.

First the meme: I thought of this meme as a way to explain volume integration by “cross sections”. 🙂 But for this post, I’ll focus on this meme showing an example of a “projection map” in mathematics. I can even provide some equations: imagine the following set in described as follows: Now the projection map to the plane is given by and the image set is which is a disk (in the yellow).

The projection onto the plane is given by and the image is which is a rectangle (in the blue).

The issue raised by this meme is that neither projection, in and of itself, determines the set . In fact, both of these projections, taken together, do not determine the object. For example: the “hollow can” in the shape of our would have the same projection; there are literally an uncountable. Example: imagine a rectangle in the shape of the blue projection joined to one end disk parallel to the yellow plane.

Of course, one can put some restrictions on candidates for (the pre image of both projections taken together); say one might want to be a manifold of either 2 or 3 dimensions, or some other criteria. But THAT would be adding more information to the mix and thereby, in a sense, providing yet another projection map.

Projections, by design, lose information.

In statistics, a statistic, by definition, is a type of projection. Consider, for example, linear regression. I discussed linear regressions and using “fake data” to teach linear regression here. But the linear regression process inputs data points and produces numbers including the mean and standard deviations of the values as well as the correlation coefficient and the regression coefficients.

But one loses information in the process. A good demonstration of this comes from Anscombe’s quartet: one has 4 very different data set producing identical regression coefficients (and yes, correlation coefficients, confidence intervals, etc). Here are the plots of the data:

And here is the data:

The Wikipedia article I quoted is pretty good; they even provide a link to a paper that gives an algorithm to generate different data sets with the same regression values (and yes, the paper defines what is meant by “different”).

Moral: when one crunches data, one has to be aware of the loss of information that is involved.

Teaching Linear Regression and ANOVA: using “cooked” data with Excel

During the linear regression section of our statistics course, we do examples with spreadsheets. Many spreadsheets have data processing packages that will do linear regression and provide output which includes things such as confidence intervals for the regression coefficients, the values, and an ANOVA table. I sometimes use this output as motivation to plunge into the study of ANOVA (analysis of variance) and have found that “cooked” linear regression examples to be effective teaching tools.

The purpose of this note is NOT to provide an introduction to the type of ANOVA that is used in linear regression (one can find a brief introduction here or, of course, in most statistics textbooks) but to show a simple example using the “random number generation” features in the Excel (with the data analysis pack loaded into it).

I’ll provide some screen shots to show what I did.

If you are familiar with Excel (or spread sheets in general), this note will be too slow-paced for you.

Brief Background (informal)

I’ll start the “ANOVA for regression” example with a brief discussion of what we are looking for: suppose we have some data which can be thought of as a set of 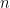points in the plane Of course the set of 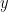values has a variance which is calculated as

It turns out that the “sum of squares” where the first term is called “sum of squares error” and the second term is called “sum of squares regression”; or: SS = SSE + SSR. Here is an informal way of thinking about this: SS is what you use to calculate the “sample variation” of the y values (one divides this term by “n-1” ). This “grand total” can be broken into two parts: the first part is the difference between the actual y values and the y values predicted by the regression line. The second is the difference between the predicted y values (from the regression) and the average y value. Now imagine if the regression slope term was equal to zero; then the SSE term would be, in effect, the SS term and the second term SSR would be, in effect, zero (). If we denote the standard deviation of the y’s by 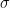then is a ratio of chi-square distributions and is therefore 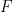with 1 numerator and denominator degrees of freedom. If or was not statistically significant, we’d expect the ratio to be small.

For example: if the regression line fit the data perfectly, the SSE terms would be zero and the SSR term would equal the SS term as the predicted y values would be the y values. Hence the ratio of (SSR/constant) over (SSE/constant) would be infinite.

That is, the ratio that we use roughly measures the percentage of variation of the y values that comes from the regression line verses the percentage that comes from the error from the regression line. Note that it is customary to denote SSE/(n-2) by MSE and SSR/1 by MSR. (Mean Square Error, Mean Square Regression).

The smaller the numerator relative to the denominator the less that the regression explains.

The following examples using Excel spread sheets are designed to demonstrate these concepts.

The examples are as follows:

Example one: a perfect regression line with “perfect” normally distributed residuals (remember that the usual hypothesis test on the regression coefficients depend on the residuals being normally distributed).

Example two: a regression line in which the y-values have a uniform distribution (and are not really related to the x-values at all).

Examples three and four: show what happens when the regression line is “perfect” and the residuals are normally distributed, but have greater standard deviations than they do in Example One.

First, I created some x values and then came up with the line . I then used the formula bar as shown to create that “perfect line” of data in the column called “fake” as shown. Excel allows one to copy and paste formulas such as these.

This is the result after copying:

Now we need to add some residuals to give us a non-zero SSE. This is where the “random number generation” feature comes in handy. One goes to the data tag and then to “data analysis”

and clicks on “random number generation”:

This gives you a dialogue box. I selected “normal distribution”; then I selected “0” of the mean and “1” for the standard deviation. Note: the assumption underlying the confidence interval calculation for the regression parameter confidence intervals is that the residuals are normally distributed and have an expected value of zero.

I selected a column for output (as many rows as x-values) which yields a column:

Now we add the random numbers to the column “fake” to get a simulated set of y values:

That yields the column Y as shown in this next screenshot. Also, I used the random number generator to generate random numbers in another column; this time I used the uniform distribution on [0,54]; I wanted the “random set of potential y values” to have roughly the same range as the “fake data” y-values.

Y holds the “non-random” fake data and YR holds the data for the “Y’s really are randomly distributed” example.

I then decided to generate two more “linear” sets of data; in these cases I used the random number generator to generate normal residuals of larger standard deviation and then create Y data to use as a data set; the columns or residuals are labeled “mres” and “lres” and the columns of new data are labeled YN and YVN.

Note: in the “linear trend data” I added the random numbers to the exact linear model y’s labeled “fake” to get the y’s to represent data; in the “random-no-linear-trend” data column I used the random number generator to generate the y values themselves.

Now it is time to run the regression package itself. In Excel, simple linear regression is easy. Just go to the data analysis tab and click, then click “regression”:

This gives a dialogue box. Be sure to tell the routine that you have “headers” to your columns of numbers (non-numeric descriptions of the columns) and note that you can select confidence intervals for your regression parameters. There are other things you can do as well.

You can select where the output goes. I selected a new data sheet.

Note the output: the value is very close to 1, the p-values for the regression coefficients are small and the calculated regression line (to generate the is:
. Also note the ANOVA table: the SSR (sum squares regression) is very, very large compared to the SSE (sum squares residuals), as expected. The variance in y values is almost completely explained by the variance in the y values from the regression line. Hence we obtain an obscenely large F value; we easily reject the null hypothesis (that ).

This is what a plot of the calculated regression line with the “fake data” looks like:

Yes, this is unrealistic, but this is designed to demonstrate a concept. Now let’s look at the regression output for the “uniform y values” (y values generated at random from a uniform distribution of roughly the same range as the “regression” y-values):

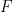Note: is nearly zero, we fail to reject the null hypothesis that and note how the SSE is roughly equal to the SS; the reason, of course, is that the regression line is close to . The calculated value is well inside the “fail to reject” range, as expected.

A plot looks like:

The next two examples show what happens when one “cooks” up a regression line with residuals that are normally distributed, have mean equal to zero, but have larger standard deviations. Watch how the values change, as well as how the SSR and SSE values change. Note how the routine fails to come up with a statistically significant estimate for the “constant” part of the regression line but the slope coefficient is handled easily. This demonstrates the effect of residuals with larger standard deviations.

Humiliated by Convex Splines

Update The writing in this article leaves something to be desired. I am going to clean this up a bit.

————————-
I was working on an analysis problem. One of the steps I needed to take was: given a set of points in the first quadrant of the standard Cartesian plane and given the fact that these points converged to the origin AND given the fact that these points met a convexity property in that for all could one then fit a convex curve though all of these points (and hence to the origin)? The answer turns out to be “no” but happily one can put an decreasing convex curve though an infinite subset of these. One standard way is to use the Beizer quadratic spline.

But I figured: “hey, we are talking about, what, a 4’th degree polynomial through two points that contains position and derivative information at the endpoints…how hard can that be?”

Then I tried it…..and found some more humility.

First I found out: it would be impossible to put a convex curve through points that had unless certain conditions were met.

Here is why: suppose The Mean Value theorem assures the existence of where which is impossible due to convexity, unless , in which case an application of the Mean Value Theorem to on (where is the first place that ) shows that convexity is impossible.

So what about a convex polynomial that runs through the first and last point of a three point convex set and has the required derivatives at the first and last point (“knot”)? It turns out that such a problem has been the focus of much research and, in general, is impossible to do (reference).

But we can get a non-polynomial function (in particular a Frobenius type polynomial with fractional powers) that yields one sided differentiability
at the first and last point, which permits appropriate “piecing together” of splines to yield a convex curve.

The key will be to show that given three knots of “convex data” and a derivative condition at the first and last knot, one can always fit in a convex “Frobenius” polynomial through the first and last knot that meet the specified derivative condition at those knots.
The set up: the last knot will be taken to be the origin; the first knot will be given in terms of the sum of two line segments; the segment ending at the origin will have the specified slope at the origin and the second segment will have the slop of the “third knot”. The missing knot (the one that the function will not run through) can be thought of as being the sum of a segment whose slope is greater than the slope at the origin along with a segment ending at the third knot whose slope is the specified slope at the third knot. Denote the first knot by and .

Theorem: Given real numbers and , there is a convex Frobenius polynomial such that:

(i)

(ii)

(iii)

(iv)

Where the derivatives in question are the appropriate one-sided derivatives.

Proof. Define .
If we can find such a that meets conditions i, ii, iii and iv with positive, convexity follows.

Set to satisfy properties i and iii.

So condition ii leads to

This leads to:

Condition iv leads to:

Or

So set

We have

This leads to the augmented matrix:

Perform the following row operation:

Now perform

Now perform

So our solution is :

Where is some real number

Note that and (as can be made as small as
desired)

Hence

Now for the term:

Now choose and

And convexity is guaranteed because the coefficients are all positive.

So now we can “piece together” as many of these splines as needed by matching the derivatives at the end points.

Next: now that we have something that works we should say something about how closely this “Frobenius polynomial” approximates the knot that it misses. That will be the subject for a subsequent post.

Probability, Evolution and Intelligent Design

I always enjoy seeing a bit of mathematics in the mainstream media. One place that it occurred was in this Jerry Coyne’s review (in New Republic magazine) of some popular “science” books which attempted to attack evolutionary theory. The review is called The Great Mutator.

Much of the review is about the mechanisms of evolution (and the ubiquitous “wind sweeping through the junkyard and making a 747” argument is demolished). But there is some mathematics used to illustrate an example:

Suppose a complex adaptation involves twenty parts, represented by twenty dice, each one showing a six. The adaptation is fueled by random mutation, represented by throwing the dice. Behe’s way of getting this adaptation requires you to roll all twenty dice simultaneously, waiting until they all come up six (that is, all successful mutations much happen together).
The probability of getting this outcome is very low; in fact, if you tossed the dice once per second, it would
take about a hundred million years to get the right outcome.
But now let us build the adaptation step by step, as evolutionary theory dictates. You start by rolling the first die, and keep rolling it until a six comes up. When it does, you keep that die (a successful first step in the adaptation) and move on to the next one. You toss the second die until it comes up six (the second step), and so on until all twenty dice show a six. On average, this would take about a hundred and twenty rolls, or a total of two minutes at one roll per second.

So, how does the mathematics work?

In the first example, the probability of getting 20 sixes in any one roll is, of course, . Then, as we repeat the experiment and stop when we get our first “all 20” outcome, we are using the geometric distribution with and the expected value to the first “success” (all 20 sixes outcome) is tries. At a rate of 1 per second, that is about 115.86 million years (using 24 hour days and 365.25 days per year).

Now if we roll the first die until the first 6 comes up, and then the second, the third, etc. and stop when we obtain the 20’th six, we are using the negative binomial distribution with . The expected value here is tries. That is a total of 2 minutes at one try per minute.

Of course it is better than that, as we’d actually be rolling the set of 20 dice until we get at least one 6, pulling out all of the sixes we get, and then rolling the remaining dice until we get at least one more 6, throwing out all of the remaining sixes, and continuing.

Working out that distribution would be an excellent exercise!

But let’s return to the negative binomial distribution versus the geometric distribution case: if the probability of a mutation is and the number of required mutations is , then the magnitude of the error as a ratio of expected values is which grows exponentially in , no matter the value of .

Note: the negative binomial distribution appears in another way: sometimes, scientists wish to calculate the number of mutations per time period. The Poisson sometimes fails because not all mutations have the same probability. So what one can do is to modify the Poisson distribution by allowing the Poisson parameter to vary as an exponential distribution; these two parameters (from the Poisson and the exponential) combine to form the two parameters for the negative binomial distribution

Instructions on how to fit the negative binomial distribution to data can be found here.