College Math Teaching

January 17, 2012

Applications of calculus in the New York Times: Comparative Statics (economics)

Filed under: applications of calculus, applied mathematics, calculus, economics, mathematical economics, media, news — oldgote @ 5:37 pm

Paul Krugman has an article that talks about the economics concept of comparative statics which involves a bit of calculus. The rough idea is this: suppose we have something that is a function of two economics variables f(x,y) and we are on some level curve: f(x,y) = C_1 at some point (x_0, y_0, f(x_0, y_0) = C) . Now if we, say, hold y constant and vary x by \Delta x what happens to the level curve C_1 ? The answer is, of course, C = C_1 + (\Delta x) \frac{\partial f}{\partial x} (x_0,y_0) + \epsilon where \epsilon is a small error that vanishes as \Delta x goes to zero; this is just multi-variable calculus and the idea of differentials, tangent planes and partial derivatives. The upshot is that the change in C , denoted by \Delta C is approximately (\Delta x) \frac{\partial f}{\partial x} (x_0,y_0) .

It isn’t every day that someone in the mainstream media brings up calculus.

January 12, 2012

So you want to take a course in complex variables

Filed under: advanced mathematics, analysis, applied mathematics, calculus, complex variables, derivatives, differential equations, integrals — collegemathteaching @ 5:30 pm

Ok, what should you have at your fingertips prior to taking such a course?

I consider the following to be minimal prerequisites:

Basic calculus

1. limits (epsilon-delta, 2-d limits)

2. limit definition of the derivative

3. basic calculus differentiation and integration formulas:
chain rule, product rule, quotient rule, integration and differentiation of polynomials, log, exponentials, basic trig functions, hyperbolic trig functions, inverse trig functions.

4. Fundamental Theorem of calculus.

5. Sequences (convergence)

6. Series: geometric series test, ratio test, comparison tests

7. Power series: interval of convergence, absolute convergence

8. Power series: term by term differentiation, term by term integrals

9. Taylor/Power series for 1/(1-x), sin(x), cos(x), exp(x)

Multi-variable calculus

1. partial derivatives

2. gradient

3. parametrized curves

4. polar coordinates

5. line and path integrals

6. conservative vector fields

7. Green’s Theorem (for integration of a closed loop in a plane)

The challenge
Some of complex variables will look “just like calculus”. And, some of the calculations WILL be “just like calculus; for example it will turn out if 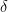\delta is any piecewise smooth curve running from z_1 to z_2 then \int_{\delta} e^z dz = e^{z_2} - e^{z_1} . But in many cases, the similarity vanishes and more care must be taken.

You will learn many things such as:
1. The complex function sin(z) is unbounded!

2. No non-constant everywhere differentiable function is bounded; compare that to f(x) = \frac{1}{1+x^2} in calculus.

3. Integrals can have some strange properties. For example, if 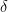\delta is the unit circle taken once around in the standard direction, \int_{\delta} Log(z) dz depends on where one chooses to start and stop, even if the start and stop points are the same!

4. You’ll come to understand why the Taylor series (expanded about 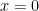x = 0 ) for \frac{1}{1+x^2} has radius of convergence equal to one…it isn’t just an artifact of the trick used to calculate the series.

5. You’ll come to understand that being differentiable on an open disk is a very strong condition for complex functions; in particular being differentiable on an open disk means being INFINITELY differentiable on that open set (compare to f(x) = x^{4/3} which has one derivative but NOT two derivatives at x = 0

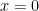
There is much more, of course.

Blog at WordPress.com.