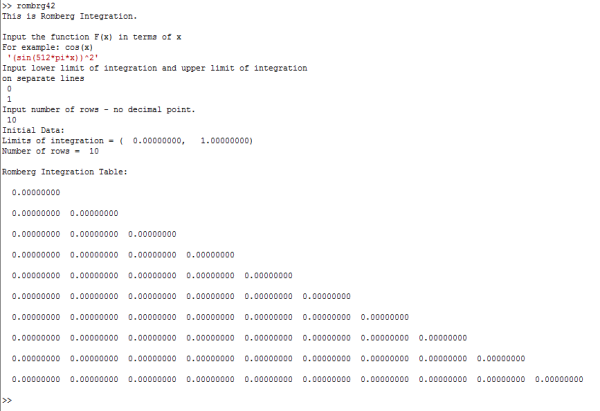
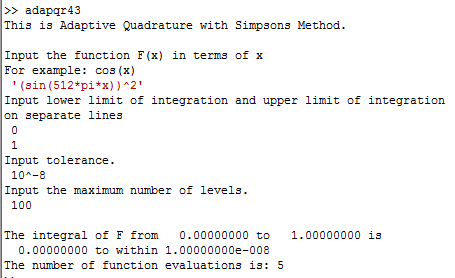
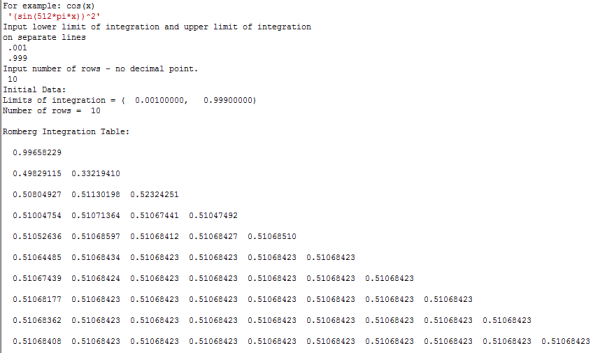
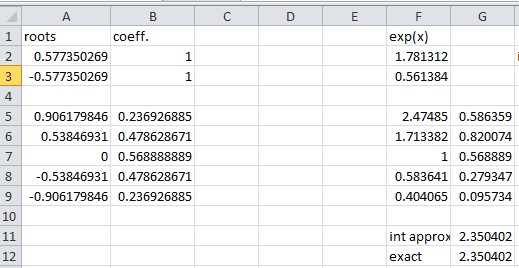
In our numerical analysis class, we are coming up on Gaussian Quadrature (a way of finding a numerical estimate for integrals). Here is the idea: given an interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D+&bg=ffffff&fg=000000&s=0&c=20201002) and a positive integer
and a positive integer 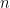 we’d like to select numbers
we’d like to select numbers ![x_i \in [a,b], i \in \{1,2,3,...n\}](https://s0.wp.com/latex.php?latex=x_i+%5Cin+%5Ba%2Cb%5D%2C+i+%5Cin+%5C%7B1%2C2%2C3%2C...n%5C%7D+&bg=ffffff&fg=000000&s=0&c=20201002) and weights
and weights  so that
so that  is estimated by
is estimated by 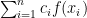 and that this estimate is exact for polynomials of degree
and that this estimate is exact for polynomials of degree 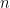 or less.
or less.
You’ve seen this in calculus classes: for example, Simpson’s rule uses  and uses
and uses  and is exact for polynomials of degree 3 or less.
and is exact for polynomials of degree 3 or less.
So, Gaussian quadrature is a way of finding such a formula that is exact for polynomials of degree less than or equal to a given fixed degree.
I might discuss this process in detail in a later post, but the purpose of this post is to discuss a tool used in developing Gaussian quadrature formulas: the Legendre polynomials.
First of all: what are these things? You can find a couple of good references here and here; note that one can often “normalize” these polynomials by multiplying by various constants.
One way these come up: they are polynomial solutions to the following differential equation: 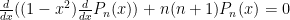 . To see that these solutions are indeed polynomials (for integer values of
. To see that these solutions are indeed polynomials (for integer values of 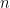 ). To see this: try the power series method expanded about
). To see this: try the power series method expanded about 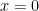 ; the singular points (regular singular points) occur at
; the singular points (regular singular points) occur at  .
.
Though the Legendre differential equation is very interesting, it isn’t the reason we are interested in these polynomials. What interests us is that these polynomials have the following properties:
1. If one uses the inner product  for the vector space of all polynomials (real coefficients) of finite degree, these polynomials are mutually orthogonal; that is, if
for the vector space of all polynomials (real coefficients) of finite degree, these polynomials are mutually orthogonal; that is, if 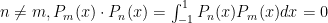 .
.
2.  .
.
Properties 1 and 2 imply that for all integers 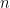 ,
,  form an orthogonal basis for the vector subspace of all polynomials of degree n or less. If follows immediately that if
form an orthogonal basis for the vector subspace of all polynomials of degree n or less. If follows immediately that if  is any polynomial of degree
is any polynomial of degree  , then
, then  (
( is a linear combination of
is a linear combination of 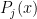 where each
where each  )
)
Now these properties can be proved from the very definitions of the Legendre polynomials (see the two references; for example one can note that  is an eigenfunction for the Hermitian operator
is an eigenfunction for the Hermitian operator 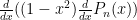 with associated eigenvalue
with associated eigenvalue 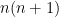 and such eigenfunctions are orthogonal.
and such eigenfunctions are orthogonal.
This little result is fairly easy to see: call the Hermitian operator 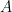 and let
and let 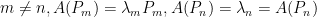 and
and  .
.
Then consider:  . But because
. But because 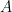 is Hermitian,
is Hermitian,  . Therefore,
. Therefore, 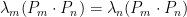 which means that
which means that 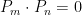 .
.
Of course, one still has to show that this operator is Hermitian and this is what the second reference does (in effect).
The proof that the operator is Hermitian isn’t hard: assume that 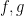 both meet an appropriate condition (say, twice differentiable on some interval containing
both meet an appropriate condition (say, twice differentiable on some interval containing ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D+&bg=ffffff&fg=000000&s=0&c=20201002) ).
).
Then use integration by parts with  :
:  . But
. But  and the result follows by symmetry.
and the result follows by symmetry.
But not every student in my class has had the appropriate applied mathematics background (say, a course in partial differential equations).
So, we will take a more basic, elementary linear algebra approach to these. For our purposed, we’d like to normalize these polynomials to be monic (have leading coefficient 1).
Our approach
Use the Gram–Schmidt process from linear algebra on the basis: 
Start with 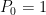 and let
and let  ; here the
; here the  are the polynomials normalized to unit length (that is,
are the polynomials normalized to unit length (that is,  . That is,
. That is, 
Next let 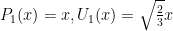
Let  Note that this is not too bad since many of the integrals are just integrals of an odd function over
Note that this is not too bad since many of the integrals are just integrals of an odd function over ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) which become zero.
which become zero.
So the general definition:
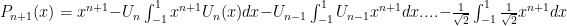
What about the roots?
Here we can establish that each 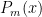 has
has 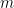 distinct, real roots in
distinct, real roots in  . Suppose
. Suppose 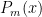 has only
has only  distinct roots of odd multiplicity in
distinct roots of odd multiplicity in  , say
, say  . Let
. Let  ; note that
; note that 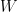 has degree
has degree  . Note that
. Note that 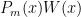 now has all roots of even multiplicity; hence the polynomial
now has all roots of even multiplicity; hence the polynomial 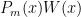 cannot change sign on
cannot change sign on ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D+&bg=ffffff&fg=000000&s=0&c=20201002) as all roots have even multiplicity. But
as all roots have even multiplicity. But  because
because 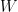 has degree strictly less than
has degree strictly less than 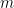 . That is impossible. So
. That is impossible. So 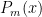 has at least
has at least 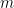 distinct roots of odd multiplicity, but since
distinct roots of odd multiplicity, but since 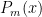 has degree
has degree  , they are all simple roots.
, they are all simple roots.