And my “clever proof” is dashed

It has been a while since I posted here, though I have been regularly posting in my complex variables class blog last semester.

And for those who like complex variables and numerical analysis, this is an exciting, interesting development.

A fundamental tension in numerical analysis is the interplay between truncation errors and rounding errors; this is particularly prevalent in the numerical approximation of #derivatives. @nhigham explores this concept in the current issue of #SIAMNews. https://t.co/QbNxAs44pN

— SIAM (@TheSIAMNews) June 6, 2018

But as to the title of my post: I was working to finish up a proof that one kind of wild knot is not “equivalent” to a different kind of wild knot and I had developed a proof (so I think) that the complement of one knot contains an infinite collection of inequivalent tori (whose solid tori contain the knot non-trivially) whereas the other kind of knot can only have a finite number of such tori. I still like the proof.

But it turns out that there is already an invariant that does the trick nicely..hence I can shorten and simplify the paper.

But dang it..I liked my (now irrelevant to my intended result) result!

A talk at University of South Alabama

My slides (in order, more or less), can be found here.

Post Promotion Summer

This is my first “terminal promotion” summer. And while I have something that I have “sort of” written up…I just don’t like the result; it basically fills in some gaps in a survey article. But I think that my thinking about this article has lead me to something that I can add to the paper so that I’ll actually LIKE what I submit.

Then again, my quandary can be summed up in this tweet:

If I wait until I am absolutely in love with my work before I send it out, it will never get sent out.

Hopefully, I’ll have more material to add to this blog this semester.

What I am working on: equivalence classes of simple closed curves; these are one to one, continuous images of the unit circle in 3-space. The objects that I am studying are so pathological that these curves fail to have a tangent at ANY point. One of these beasts can be constructed by taking the intersection of these nested, solid tori.

Pop-math: getting it wrong but being close enough to give the public a feel for it

Space filling curves: for now, we’ll just work on continuous functions .

A curve is typically defined as a continuous function where is, say, a manifold (a 2’nd countable metric space which has neighborhoods either locally homeomorphic to or . Note: though we often think of smooth or piecewise linear curves, we don’t have to do so. Also, we can allow for self-intersections.

However, if we don’t put restrictions such as these, weird things can happen. It can be shown (and the video suggests a construction, which is correct) that there exists a continuous, ONTO function ; such a gadget is called a space filling curve.

It follows from elementary topology that such an cannot be one to one, because if it were, because the domain is compact, would have to be a homeomorphism. But the respective spaces are not homeomorphic. For example: the closed interval is disconnected by the removal of any non-end point, whereas the closed square has no such separating point.

Therefore, if is a space filling curve, the inverse image of a points is actually an infinite number of points; the inverse (as a function) cannot be defined.

And THAT is where this article and video goes off of the rails, though, practically speaking, one can approximate the space filling curve as close as one pleases by an embedded curve (one that IS one to one) and therefore snake the curve through any desired number of points (pixels?).

So, enjoy the video which I got from here (and yes, the text of this post has the aforementioned error)

Student integral tricks…

Ok, classes ended last week and my brain is way out of math shape. Right now I am contemplating how to show that the complements of this object

and of the complement of the object depicted in figure 3, are NOT homeomorphic.

I can do this in this very specific case; I am interested in seeing what happens if the “tangle pattern” is changed. Are the complements of these two related objects *always* topologically different? I am reasonably sure yes, but my brain is rebelling at doing the hard work to nail it down.

Anyhow, finals are graded and I am usually treated to one unusual student trick. Here is one for the semester:

Now I was hoping that they would say at which case the integral is translated to: which is easy to do.

Now those wanting to do it a more difficult (but still sort of standard) way could do two repetitions of integration by parts with the first set up being and that works just fine.

But I did see this: (ok, there are some domain issues here but never mind that) and we end up with the transformed integral: which can be transformed to by elementary trig identities.

And yes, that leads to an answer of which, upon using the triangle

Gives you an answer that is exactly in the same form as the desired “rationalization substitution” answer. Yeah, I gave full credit despite the “domain issues” (in the original integral, it is possible for ).

What can I say?

A popular video and covering spaces…

Think back to how you introduced the sine and cosine functions on the real line. Ok, you didn’t do it quite this way, but what you did, in effect, is to define and and then use “elementary trigonometry” to relate the “angle” to the arc length subtended on the circle . One notes that the map defined by has period

Note: the direction “to the right” on the real line is taken to be “counterclockwise” on the circle (red arrows).

Skip if you haven’t had a topology class
The top line is known as the “universal covering space” for the circle. The reason for the terminology has to do with topology. Depending on how long ago you had your topology course, you might remember that the fundamental group of the real line is trivial and the associated group of deck transformations is infinite cyclic (generated by the map ). One then shows that the fundamental group of the circle is the quotient of the group of deck transformations with the fundamental group of the real line; hence the fundamental group of the circle is infinite cylic.

Resume if you haven’t had a topology class

Notice the following: if one, say, “takes a walk” along the line in the direction of the red arrow, the action of the “covering mapping” is to take the same walk in the counter clockwise direction of the circle. That is, the covering action does the following: a walk on the line in the direction of points corresponds to a walk on the circle . That is, walking from to corresponds to a complete lap of the circle.

(that is, on the real line, )

Now note the following: for BOTH the line and the circle, the direction is well defined. “To the right” on the real line” is “counter clockwise” on the circle.

However: on the real line, it makes perfect sense to say that is “before” which is “before” which is “before” and so on; this is merely:

. This is order is valid no matter where one starts on the line.

However, this “universal ordering” makes no sense on the circle, UNLESS one specifies a start point. True, one moves from 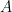to to and back to 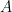again..but if one started at and started to walk, it would appear that 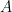came AFTER and not before.

So what?

A friend posted this to her facebook wall:

This quirky animation from CraveFX starts off innocently enough, a janitorial worker mops up a leaky refrigerator and then picks up a coin on the ground. It’s not until you see what causes the refrigerator to leak and why the coin is on the ground that you realize that you’re watching an intricate moving puzzle piece before your eyes. The characters are stuck in an infinite loop caused by another character in their own infinite loop. It’s chaotic and great and hard to keep up with.

The video is below. Now the question: “what action occurred before what other action”? and the answer is “it depends on when you started watching”. The direction of time corresponds to the red arrows in the above diagrams; THAT is well defined. Why? The reason is the Second Law of Thermodynamics; spills do NOT reverse themselves, hence the direction is set in stone, so to speak. But as far as order, it depends ON WHEN THE VIEWER STARTED WATCHING.

Anyway, this video reminded me of covering spaces.

A quick break from the routine…

This came as an advertisement. I got some good natured ribbing.

But this semester, I’ve been up to my eyeballs in this new (to me) course. If I never see actuarial mathematics again, it will be too soon. 🙂

Embarrassing gaps in my mathematical knowledge

Yes, mathematics is a huge, huge subject and no one knows everything. And, when I was a graduate student, I could only focus on 1-2 advanced courses at a time, and when I was working on my thesis, I almost had a “blinders on” approach to finishing that thing up. I think that I had to do that, given my intellectual limitations.

So, even in “my area”, my knowledge outside of a very narrow area was weak at best.

Add to this: 20+ years of teaching 3 courses per semester; I’ve even forgotten some of what I once knew well, though in return, I’ve picked up elementary knowledge in disciplines that I didn’t know before.

But, I have many gaps in my own “area”. One of these is in the area of hyperbolic geometry and the geometry of knot complements (think of this way: take a smooth simple closed curve in , add a point at infinity to get (a compact space), now take a solid torus product neighborhood of the knot (“thicken” the knot up into a sort of “rope”) then remove this “rope” from . What you have left over is a “knot complement” manifold.

Now these knot complements fall into one of 3 different types: they are torus knot complements (the knot can live on the “skin” of a torus),

satellite knot complements (the knot can live inside the solid torus that is the product neighborhood of a different, mathematically inequivalent knot,

or the knot complement is “hyperbolic”; it can be given a hyperbolic structure. At least for “most” knots of small “crossing number” (roughly: how many crossings the knot diagram has), are hyperbolic knots.

So it turns out that the complement of such knots can be filled with “horoballs”; roughly speaking, these are the interior of spheres which are “tangent to infinity”; infinity is the “missing stuff” that was removed when the knot was removed from . And, I really never understood what was going on at all.

I suppose that one can view the boundary of these balls (called “horospheres”) as one would view, say, the level planes in ; those planes become spheres when the point at infinity is added. This is a horoball packing of the complement of the figure 8 knot; missing is the horosphere at which can be thought of as a plane.

But the internet is a wonderful thing, and I found a lecture based on the work of Anastasiia Tsvietkova and Morwen Thistlethwaite (who generated the horoball packing photo above) and I’ll be trying to wrap my head around this.

Workshop in Geometric Topology: TCU 2015 morning session 1

I’ll be blunt: I’ve been teaching at a 11-12 hour load (mostly 11; one time I had a 9 hour load; 3 courses) since fall, 1991. Though I’ve published, most of what I’ve done has been extremely “bare handed”; it is tough to learn the most advanced techniques (which is a full time job in and of itself)

So, at math conferences, I get to see how much further behind I’ve fallen.

But these things help in the following way:

1. They are an excellent change of pace from the usual routine of teaching calculus.
2. I do learn things, even if it is “looking up” a definition or two; for example I looked up the definition of “pure braid group” in between the 20 minute talks.
3. I have to review my own stuff to see if I am indeed making progress; I don’t want to say something idiotic in front of some very smart, informed people.

But yes, the talks have been given by smart, (mostly) young, energetic people who have been studying the topic that they are talking about very intensely for a long time; frequently it is tough to hang in to the second half of the 20 minute talks. But I can see WHAT is being studied, what tools are being used and, as I said before, find stuff to look up.

The final talk: didn’t understand much beyond the general gist but it was well organized, well presented..exactly what you get when you have a brilliant energetic young researcher working full time in mathematical research.

On one hand, I envy his talent. On the other hand, I am glad that we have some smart humans among us; they benefit all of us.

The trip here The plane was about 2.5 hours late getting in, then there was a long ride to the car rental place and a 35 minute drive to campus, then finding my way around in the dark. So no morning run; I might do a gentle “after the talks” focused walk (5K-ish?).

I talk at 9 am tomorrow and I want to make it worth their while.

And a Fields Medalist makes me feel better

I have subscribed to Terence Tao’s blog.

His latest post is about a clever observation about…calculus: in particular is is about calculating:

for . Try this yourself and surf to his post to see the “slick, 3 line proof”.

But that really isn’t the point of this post.

This is the point: I often delight in finding something “fun” and “new to me” about an established area. I thought “well, that is because I am too dumb to do the really hard stuff.” (Yes, I’ve published, but my results are not Annals of Mathematics caliber stuff. 🙂 )

But I see that even the smartest, most accomplished among us can delight in the fun, simple things.

That makes me feel better.

Side note: I haven’t published much on this blog lately, mostly because I’ve been busy updating this one. It is a blog giving notes for my undergraduate topology class. That class was time consuming, but I had the teaching time of my life. I hope that my students enjoyed it too.