Rant: reviewing job applications.

The good news: we are hiring (that means we aren’t letting faculty go! 🙂 )

The bad news: that means reviewing a ton of applications over break.

Just a hint: if you are leaving your current tenure track job (at a school regarded as a “public Ivy”) so you can have “more time and resources to research”, please don’t apply to a undergraduate institution where the load is 11-12 contact hours per semester, in addition to endless administrative duties.

Here, you’ll spend at least some of your time dealing with students who complain about being marked off for saying ….in a so called calculus class!

Sigh…

Rant: please stop with the teaching of “gimmicks for calculation”

I finished teaching calculus II (our course: techniques for integration, applications of integrals and infinite sequences/series) and noticed that some of our freshmen students came in knowing how to do many of the calculations…did well on the first exam…then didn’t do so well in the rest of the course.

Evidently, they were well versed in calculation tricks learned in high school; give them and they could whip out a table.

So here is my rant: we teach integration by parts not so much to calculate integrals like (which can be rapidly done with a calculator) but rather so they can understand the technique of integration by parts.

Why? Well, there are many uses of integration by parts and I’ll just display a few uses of them:

1. Taylor Polynomials. How do we get these? If we assume that has enough derivatives, we proceed in the following manner: calculate in two different ways: use the Fundamental Theorem of calculus on one side (to obtain and use integration by parts on the other side: (yes, we are being choosy about which anti derivative of to use).
This means: so and one proceeds from there.

2. Differential equations: given one seeks to find an integrating factor (which is so as to get:

which can be written as . That is, the left hand side is just the product rule for derivatives, which, as you know (if you are a calculus teacher), is really all integration by parts is!

Sure, one can jazz it up (as we subtly did in the Taylor Polynomial calculation); the integration by parts formula is really where are arbitrary constants. But, my main point is that integration by parts should be UNDERSTOOD; short cuts to do tedious calculations are relatively unimportant, IMHO.

Now if you want to ask students “why does tabular integration work”, then….GREAT!

Oldie but goodie: Physics professor discovers that some disassociate grades with performance.

I shall post this article on my class websites:

What alarms me is their indifference toward grades as an indication of personal effort and performance. Many, when pressed about why they think they deserve a better grade, admit they don’t deserve one but would like one anyway. Having been raised on gold stars for effort and smiley faces for self-esteem, they’ve learned that they can get by without hard work and real talent if they can talk the professor into giving them a break. This attitude is beyond cynicism. There’s a weird innocence to the assumption that one expects (even deserves) a better grade by begging for it. With that outlook, I guess I shouldn’t be as flabbergasted as I was that 12 students asked me to change their grades after final grades were posted.
That’s 10 percent of my class who let three months of midterms, quizzes and lab reports slide until long past remedy. My graduate student calls it hyperrational thinking: if effort and intelligence don’t matter, why should deadlines? What matters is getting a better grade through an unearned bonus, the academic equivalent of a freebie T-shirt or toaster giveaway. Rewards are disconnected from the quality of one’s work. An act and its consequences are unrelated, random events.

Their arguments for wheedling better grades often ignore academic performance. Perhaps they feel it’s not relevant. “If my grade isn’t raised to a D, I’ll lose my scholarship.” “If you don’t give me a C, I’ll flunk out.” One sincerely overwrought student pleaded, “If I don’t pass, my life is over.” […]

Most of my students are science and engineering majors. If they’re good at getting partial credit but not at getting the answer right, then the new bridge breaks or the new drug doesn’t work. One finds examples here in Atlanta. Last year a light tower in the Olympic Stadium collapsed, killing a worker. It collapsed because an engineer miscalculated how much weight it could hold. A new 12-story dormitory could develop dangerous cracks due to a foundation that’s uneven by more than six inches. The error resulted from incorrect data being fed into a computer. I drive past that dorm daily on my way to work, wondering if a foundation crushed under kilotons of weight is repairable or if this structure will have to be demolished. Two 10,000-pound steel beams at the new Aquatic Center collapsed in March, crashing into the Student Athletic Complex. (Should we give partial credit since no one was hurt?) Those are real-world consequences of errors and lack of expertise.
But the lesson is lost on the grade-grousing 10 percent. Say that you won’t (not can’t, but won’t) change the grade they deserve to what they want, and they’re frequently bewildered or angry. They don’t think it’s fair that they’re judged according to their performance, not their desires or “potential.” They don’t think it’s fair that they should jeopardize their scholarships or be in danger of flunking out simply because they could not or did not do their work. But it’s more than fair; it’s necessary to help preserve a minimum standard of quality that our society needs to maintain safety and integrity.

Semester grades are out…

Cue e-mail messages saying “professor, I’d like to meet you over semester break to “discuss” my grade.”

Cue my answer:

I do tell them I’d be happy to meet with them at the start of the next semester to SEE their final exam…I’ll even give them a copy. I’ll be happy to discuss how they can improve their performances and to enhance their mastery of the material.

And yes, I give them their test averages prior to the final exam so they can check to see if I have the grades recorded correctly.

But the reality is that many have no interest in improving their performance; they merely want a higher evaluation given to their current performance.

That is human nature, I think. Fair evaluation of one’s performance can be painful…for ALL of us.

Teaching the basics of numerical methods for solving differential equations

This semester we had about a week to spend on numerical methods. My goal was to give them the basics of how a numerical method works: given one selects a step size and then one rides the slope of the tangent line: and repeat the process. This is the basic Euler method; one can do an averaging process to get a better slope (Runge-Kutta) and one, if one desires, can use previous points in a multi-step process (e. g. Adams-Bashforth, etc.). Ultimately, it is starting at a point and using the slope at that point to get a piece wise linear approximation to a solution curve.

But the results of such a process confused students. Example: if one used a spreadsheet to do the approximation process (e. g. Euler or Runge-Kutta order 4), one has an output something like this:

So, there is confusion. They know how to get from one row to the other and what commands to type. But….”where is the solution?” they ask.

One has to emphasize what is obvious to us: the columns, is the approximate solution…a piece wise approximation of one anyway. What we have is a set where these ordered pairs are points in the approximate solution to the differential equation that runs through those points. One cannot assume that the students understand this, even when they can do the algorithm.

An Exam Question

As a bonus question, I gave the following graph:

I then said: “I was testing out an Euler method routine on the differential equation and I got the following output.

A) Is this solution mathematically possible?

B) If there is an error, is this an error induced by the Euler method or by an improper step size, or is a coding error more likely?

Many students got part A correct: some noted that is an equilibrium solution and that this differential equation meets the “existence and uniqueness” criteria everywhere; hence the graph of the proposed solution intersecting the equilibrium solution is impossible.

Others noted that the slope of a solution at would be zero; others noted that the slopes above were negative and this proposed solution leveled out. Others noted that is an attractor hence any solution near would have to stay near there.

But no one got part B; one even went as far to say that someone with a Ph. D. in math would never make such an elementary coding error (LOL!!!!!)

But the key here: the slopes ARE negative above and a correct Euler method (regardless of step size…ok, within reason) would drive the curve down.

So this WAS the result of a coding error.

What went wrong: I was running both RK-order 4 and Euler (for teaching purposes) and I stored the RK slope with one variable and calculated the “new Y” using the RK slope (obtained from the RK approximation) for the Euler method. Hence when the curve “jumped over” the , the new slope it picked up was a near zero slope from the RK approximation for the same value of 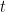(which was near, but below the equilibrium.

My problem is that the two variables in the code differed by a single number (my bad). I was able to fix the problem very quickly though.

An aside
On another part of the test, I told them to solve and gave them the phrase: “hint: THINK first; this is NOT a hard calculation”. A few students got it, but mostly the A students. There was ONE D student who got it right!

Have you ever had a student like this one?

I am grading differential equations final exams. I have the usual mix…for the most part.

But I have 3 students who are very, very good. And as far as one of these: let’s just say that when he/she writes an answer down that differs from the one I produced for the key…I double check my own work.

And once in a while….I am quietly embarrassed. 🙂

Note: but even this student is confused about numerical methods to solve differential equations; I’ll have to address that (with a post) over break.