The Dirac Delta Function in Differential Equations
The delta ”function” is often introduced into differential equations courses during the section on Laplace transforms. Of course the delta
”function” isn’t a function at all but rather what is known as a ”distribution” (more on this later)
A typical introduction is as follows: if one is working in classical mechanics and one applies a force 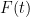 to a constant mass
to a constant mass  at time
at time  then one can define the impulse
then one can define the impulse 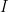 of
of  over an interval
over an interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) by
by  where
where  is the velocity. So we can do a translation to set
is the velocity. So we can do a translation to set 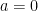 and then consider a unit impulse and vary
and then consider a unit impulse and vary 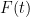
according to where 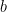 is; that is, define
is; that is, define

Then  is the force function that produces unit impulse for a given
is the force function that produces unit impulse for a given 
Then we wave our hands and say  (this is a great reason to introduce the concept of the limit of functions in a later course) and then argue that for all functions that are continuous over an interval containing 0,
(this is a great reason to introduce the concept of the limit of functions in a later course) and then argue that for all functions that are continuous over an interval containing 0,
 .
.
The (hand waving) argument at this stage goes something like: ”the mean value theorem for integrals says that there is a 
between 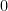 and
and  such that
such that  Therefore as
Therefore as 
 by continuity. Therefore we can define the Laplace transform
by continuity. Therefore we can define the Laplace transform  ”
”
Illustrating what the delta ”function” does.
I came across this example by accident; I was holding a review session for students and asked for them to give me a problem to solve.
They chose  (I can remember what
(I can remember what  and
and 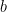 were but they aren’t important here as we will see) with initial conditions
were but they aren’t important here as we will see) with initial conditions 
So using the Laplace transform, we obtained:

But with  this reduces to
this reduces to 
In other words, we have the ”same solution” as if we had  with
with  .
.
So that might be a way to talk about the delta ”function”; it is exactly the ”impulse” one needs to ”cancel out” an initial velocity of 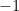 or,
or,
equivalently, to give an initial velocity of 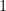 and to do so instantly.
and to do so instantly.
Another approach to the delta function
Though it is true that  for all
for all  and
and
 by design, note that
by design, note that  fails to be continuous at
fails to be continuous at 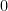 and at
and at  .
.
So, can we obtain the delta ”function” as a limit of other functions that are everywhere continuous and differentiable?
In an attempt to find such a family of functions, It is a fun exercise to look at a limit of normal density functions with mean zero:
 . Clearly for all
. Clearly for all
 and
and  .
.
Here is the graph of some of these functions: we use  ,
,  and
and  respectively.
respectively.

Calculating the Laplace transform


Do some algebra to combine the exponentials, complete the square and do some algebra to obtain:
![\frac{1}{\sigma \sqrt{2\pi }}\int_{0}^{\infty }\exp (-\frac{1}{2\sigma ^{2}}(t+\sigma ^{2}s)^{2})\exp (\frac{s^{2}\sigma^{2}}{2})dt=\exp (\frac{s^{2}\sigma ^{2}}{2})[\frac{1}{\sigma \sqrt{2\pi }}\int_{0}^{\infty }\exp (-\frac{1}{2\sigma ^{2}}(t+\sigma^{2}s)^{2})dt]](https://s0.wp.com/latex.php?latex=%5Cfrac%7B1%7D%7B%5Csigma+%5Csqrt%7B2%5Cpi+%7D%7D%5Cint_%7B0%7D%5E%7B%5Cinfty+%7D%5Cexp+%28-%5Cfrac%7B1%7D%7B2%5Csigma+%5E%7B2%7D%7D%28t%2B%5Csigma+%5E%7B2%7Ds%29%5E%7B2%7D%29%5Cexp+%28%5Cfrac%7Bs%5E%7B2%7D%5Csigma%5E%7B2%7D%7D%7B2%7D%29dt%3D%5Cexp+%28%5Cfrac%7Bs%5E%7B2%7D%5Csigma+%5E%7B2%7D%7D%7B2%7D%29%5B%5Cfrac%7B1%7D%7B%5Csigma+%5Csqrt%7B2%5Cpi+%7D%7D%5Cint_%7B0%7D%5E%7B%5Cinfty+%7D%5Cexp+%28-%5Cfrac%7B1%7D%7B2%5Csigma+%5E%7B2%7D%7D%28t%2B%5Csigma%5E%7B2%7Ds%29%5E%7B2%7D%29dt%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Now do the usual transformation to the standard normal random variable via 
And we obtain:
 for all
for all  . Note: assume
. Note: assume  and that
and that 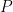 is shorthand for the usual probability distribution function.
is shorthand for the usual probability distribution function.
Now if we take a limit as 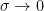 we get
we get 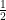 on the right hand side.
on the right hand side.
Hence, one way to define 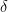 is as
is as  . This means that while
. This means that while
 is off by a factor of 2,
is off by a factor of 2,
 as desired.
as desired.
Since we now have derivatives of the functions to examine, why don’t we?
 which is zero at
which is zero at 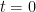 for all
for all  But the behavior of the derivative is interesting: the derivative is at its minimum at
But the behavior of the derivative is interesting: the derivative is at its minimum at  and at its maximum at
and at its maximum at  (as we tell our probability students: the standard deviation is the distance from the origin to the inflection points) and as
(as we tell our probability students: the standard deviation is the distance from the origin to the inflection points) and as  the inflection points get closer together and the second derivative at the
the inflection points get closer together and the second derivative at the
origin approaches  which can be thought of as an instant drop from a positive velocity at
which can be thought of as an instant drop from a positive velocity at 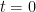 .
.
Here are the graphs of the derivatives of the density functions that were plotted above; note how the part of the graph through the origin becomes more vertical as the standard deviation approaches zero.






