I still remember one of the more moronic things I have ever written on an exam; I said “Set E has measure zero and is therefore countable….”. My professor wrote “whatever happened to the Cantor Set”, which he had told us about and had covered extensively.
It was one of those things that I had heard but really didn’t internalize into a working part of my mathematical mind; the latter is difficult to do.
So what is a Cantor Set? Actually, it depends on who you ask. 🙂 A topologist is likely to give a different answer than an analyst; I’ll discuss what is going on.
First, I’ll construct the traditional Middle Thirds Cantor Set; this is an example of a subset of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D+&bg=ffffff&fg=000000&s=0&c=20201002) which
which
1. Has Lebesgue outer measure zero (and is therefore measurable)
2. Is uncountable.
It also has some other interesting properties and can be generalized; as George Simmons in Introduction to Topology and Modern Analysis says on page 68:
[…] the Cantor set is a very intricate mathematical object and is just the sort of thing that mathematicians delight in.
Descriptions: I’ll describe the Cantor set by describing what is NOT in it: the intervals  . Or, I can describe it as an intersection of closed sets:
. Or, I can describe it as an intersection of closed sets: ![C_{1} = [0,1/3] \cup [2/3,1], C_{2} = [0, 1/9] \cup [2/9, 1/3] \cup [2/3,7/9] \cup [8/9,1],...](https://s0.wp.com/latex.php?latex=C_%7B1%7D+%3D+%5B0%2C1%2F3%5D+%5Ccup+%5B2%2F3%2C1%5D%2C+C_%7B2%7D+%3D+%5B0%2C+1%2F9%5D+%5Ccup+%5B2%2F9%2C+1%2F3%5D+%5Ccup+%5B2%2F3%2C7%2F9%5D+%5Ccup+%5B8%2F9%2C1%5D%2C...&bg=ffffff&fg=000000&s=0&c=20201002) and then the Cantor set
and then the Cantor set  . Another way of describing the Cantor middle thirds set is the set of numbers whose base three fraction expansion does not contain the digit “1” anywhere (as these numbers lie in the removed intervals, always the middle third).
. Another way of describing the Cantor middle thirds set is the set of numbers whose base three fraction expansion does not contain the digit “1” anywhere (as these numbers lie in the removed intervals, always the middle third).
Some facts are immediate: The Cantor set is closed as its complement is the union of open sets. It is bounded and hence compact. The middle thirds Cantor set has measure zero; here is why: if we add the measures of the complement: 
But the Cantor set is uncountable! This can be seen in many ways; there is a topological proof; we’ll present a brute force one.
Let  denote the Cantor middle thirds set and let
denote the Cantor middle thirds set and let  . Note that each
. Note that each  consists of
consists of  disjoint intervals of length
disjoint intervals of length  . Now we will map
. Now we will map  to a point on the sequence of 1’s and 0’s:
to a point on the sequence of 1’s and 0’s:  where
where  if
if  and 1 if
and 1 if  . Then
. Then  if
if  is in the first third of the next interval and 1 if it is in the final third. We do this at every stage and note that the map from
is in the first third of the next interval and 1 if it is in the final third. We do this at every stage and note that the map from  onto the sequence is onto. The map is also one to one because if
onto the sequence is onto. The map is also one to one because if  then they are at least
then they are at least  apart, and choose a non-deleted interval that is shorter than this
apart, and choose a non-deleted interval that is shorter than this  ; that interval cannot contain both
; that interval cannot contain both  and
and 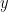 .
.
We can say much more about the Cantor set(s); I’ll conclude with a few interesting tidbits:
1. It isn’t that tough to exhibit some elements of  that are NOT endpoints of deleted intervals; merely choose a base three fraction sum that does not contain 1’s in its numerator. Here is one example: choose
that are NOT endpoints of deleted intervals; merely choose a base three fraction sum that does not contain 1’s in its numerator. Here is one example: choose

2. One can alter the construction of the Cantor middle third set to obtain a Cantor set of any measure less than 1: do the same middle thirds construction but ensure that the length of each removed interval is  at stage
at stage 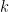 Then one can compute the length of the removed intervals:
Then one can compute the length of the removed intervals:
 . Now if
. Now if  is the desired measure of the complement (less than 1, of course), one solves
is the desired measure of the complement (less than 1, of course), one solves  for
for 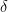 to obtain
to obtain  . One notes that
. One notes that  yields
yields  .
.
The Cantor set (of any measure) has some interesting properties. For one, every point is a limit point (remember, it has the subspace topology). This isn’t hard to see; let  be a neighborhood of any point
be a neighborhood of any point  of the Cantor set of width
of the Cantor set of width  and let
and let 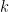 be such that
be such that  . Then this non-deleted interval containing
. Then this non-deleted interval containing  must lie in
must lie in 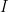 , which means that
, which means that  contains other points of the Cantor set. This property is called “being dense in itself”. This property, plus being compact, is enough to prove that the set is uncountable.
contains other points of the Cantor set. This property is called “being dense in itself”. This property, plus being compact, is enough to prove that the set is uncountable.
The Cantor set is totally disconnected; that is, the only connected components are one point sets. This is why: given any two different points in a Cantor set, there is a deleted interval between them.
Note: it might not make sense to talk of THE Cantor set as one can construct Cantor sets of different measures. But it does make sense to talk about the Cantor set in terms of topology as every compact, dense in itself, totally disconnected metric space is homeomorphic (in fact, homeomorphic to the countably infinite product of  where every factor has the discrete topology and the whole space has the product topology. Note: sometimes this topological space is referred to as the Cantor SPACE with Cantor SET being reserved for middle thirds type of construction.
where every factor has the discrete topology and the whole space has the product topology. Note: sometimes this topological space is referred to as the Cantor SPACE with Cantor SET being reserved for middle thirds type of construction.
Astonishingly, every compact metric space is the image of the Cantor space (and therefore of the Cantor set); that is a topic for a later time.
What does this have to do with integration?
Remember that the standard Cantor middle thirds set has measure zero; hence two functions defined on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D+&bg=ffffff&fg=000000&s=0&c=20201002) that are equal except on the Cantor set have equal integrals; we will also see that the Cantor set can cause some mischief when we start talking about the Fundamental Theorem of Calculus. 🙂
that are equal except on the Cantor set have equal integrals; we will also see that the Cantor set can cause some mischief when we start talking about the Fundamental Theorem of Calculus. 🙂
If you can’t wait, see here.
is continuous at
if
which means that the limit exists and is equal to the function evaluated at the point. In analysis notation: for all
there exists
such that
whenever
.
containing
,
is an open set. But never mind that for now.
for
rational and
for
irrational.
for
and zero at
.
:
for
and zero at
.
for
and zero at
.
for
rational, and
for
irrational.
, has derivative equal to zero almost everywhere, and yet increases from 0 to 1.