My Ph. D. basic math classes were a long time ago; in the fall of 1985 I enrolled in the beginning topology, algebra, analysis and algebraic topology classes. The algebra, analysis and topology classes were designed to get the student through the preliminary examinations.
The ironic thing is that while I passed analysis on my first try (summer of1986) and algebra on the first try (summer of 1987), it took me three tries to get through topology which I finally passed in the winter of 1988. Of course, that is what I ended up specializing in.
But I can honestly say that most of my analysis was ”studying the problems that might appear on the exam”; I really didn’t know what I was doing nor did I understand the material. I had no perspective whatsoever; I really didn’t know where the course was going. Therefore I remember almost none of it.
What does this have to do with the teaching of college mathematics? I see it this way: often, prior to tackling an abstract concept (say, Lebesgue Integration), one first assembles some tools (say, measure theory, the concept of a sigma algebra of sets, Borel sets, etc.) and then uses these tools as the need arises. But the tools are often developed without any context; I didn’t see why any of this was needed or what it would be used for. I had no perspective; I didn’t know WHY I had to be patient with these esoteric (to me at that time) tools.
So, what I remember now is to constantly remind the students where we are going with a topic; I try to explain WHY we need to be patient with this piece of drudgery or that.
Lebesgue Integration
My goal: I hope to review Lebesgue integration for my own benefit and hopefully, via some notes, perhaps provide some perspective for the student who is going through this process for the first time.
For my references, I am choosing A Primer of Lebesgue Integration by H. S. Bear and Real Analysis by H. L. Royden.
Why Lebesgue Integration?
Ground Rules
For the duration, I’ll be discussing the integration of positive functions over a closed, bounded interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) . In fact, I’ll go ahead and use
. In fact, I’ll go ahead and use ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) with no loss of generality.
with no loss of generality.
Of course, if we are merely concerned with integrating functions which are piecewise continuous then the Riemann integral (say, as defined as the limit of upper and lower sums) works just fine.
However what happens if we want to, say, extend the class of functions that we can integrate?
Suppose, for example, we wish to compute  or attempt to compute
or attempt to compute  ?
?
Ok, strictly speaking, these functions aren’t defined on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) , so we can replace the integrand by, say a conditional function:
, so we can replace the integrand by, say a conditional function:
 in the first case and similarly in the second case.
in the first case and similarly in the second case.
Of course, we tell our students that while these functions are NOT Riemann integrable (unbounded functions aren’t as the upper sum will never be finite for any finite partition), we can possibly extend the notion of integrability by using the improper integral technique, which, of course, shows that the first integral converges and the second one does not.
But again, we have a type of piecewise continuity. What happens when we don’t?
Let us examine another couple of functions:


Notice that 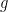 is bounded whereas
is bounded whereas 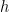 is not. Notice that neither is Riemann integrable as there is no hope of a upper and lower sums converging. But notice something else: we know that the rationals compose a minescule portion of the real numbers; hence there might be another theory of integration that would all us to integrate both of these functions and obtain 0 for the integral. But there isn’t a good way to obtain the integrals of these functions as a limit of Riemann integrals; there are no smaller intervals to work with. Hence the need for a more expansive theory of integration.
is not. Notice that neither is Riemann integrable as there is no hope of a upper and lower sums converging. But notice something else: we know that the rationals compose a minescule portion of the real numbers; hence there might be another theory of integration that would all us to integrate both of these functions and obtain 0 for the integral. But there isn’t a good way to obtain the integrals of these functions as a limit of Riemann integrals; there are no smaller intervals to work with. Hence the need for a more expansive theory of integration.
About the rational numbers: why do they ”take up little space”? I’ll assume that the reader knows that the rationals are countable and the reals are not, hence there are many more irrational numbers than rational ones.
But as far as ”taking up space”: what do we mean by that? We will answer this when we develop ”measure theory”; that is, a way of assigning a generalization of a “length” to more complicated subsets of the real line. For now I’ll explain why the set of rational numbers doesn’t take up much space, even though they are a dense subset of the real line.
I will show that we can cover all of the rationals by a countable set of intervals whose lengths add up to an arbitrarily small number. That is,
for any given  I’ll construct a countable set of intervals
I’ll construct a countable set of intervals ![[a_{i},b_{i}]](https://s0.wp.com/latex.php?latex=%5Ba_%7Bi%7D%2Cb_%7Bi%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that
such that ![\cup _{i=1}^{\infty}[a_{i},b_{i}]](https://s0.wp.com/latex.php?latex=%5Ccup+_%7Bi%3D1%7D%5E%7B%5Cinfty%7D%5Ba_%7Bi%7D%2Cb_%7Bi%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) contains ALL of the rational numbers AND
contains ALL of the rational numbers AND  Of course, these intervals are NOT disjoint; far from it. But their union contains all of the rational numbers.
Of course, these intervals are NOT disjoint; far from it. But their union contains all of the rational numbers.
Review: Recall  for
for 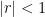 .
.
Let  be the set of rational numbers (which are countable). Then for
be the set of rational numbers (which are countable). Then for  consider the interval
consider the interval ![[q_{k}-\frac{1}{2}(\frac{\varepsilon +1}{\varepsilon })^{k},q_{k}+\frac{1}{2}(\frac{\varepsilon+1}{\varepsilon })^{k}]](https://s0.wp.com/latex.php?latex=%5Bq_%7Bk%7D-%5Cfrac%7B1%7D%7B2%7D%28%5Cfrac%7B%5Cvarepsilon+%2B1%7D%7B%5Cvarepsilon+%7D%29%5E%7Bk%7D%2Cq_%7Bk%7D%2B%5Cfrac%7B1%7D%7B2%7D%28%5Cfrac%7B%5Cvarepsilon%2B1%7D%7B%5Cvarepsilon+%7D%29%5E%7Bk%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) . This interval has length
. This interval has length 
Hence adding the lengths of the intervals together is the same as  . So the sum of the lengths of closed intervals which covers all of the rationals can be made as small as desired.
. So the sum of the lengths of closed intervals which covers all of the rationals can be made as small as desired.
So, getting back to the problem of integration: how do we do this? The idea behind the Lebesgue integral is to first define this integral for
“simple functions” that is, functions that take on precisely one value over a set. For example: a step function can be thought of as a kind of
sum of simple functions.
Then  is a simple function over a set
is a simple function over a set 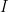 and
and  is the “measure”; (a kind of length) of
is the “measure”; (a kind of length) of 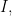 then the new integral would be defined as
then the new integral would be defined as  (think of the integral in terms of “area”; and this would be a height (in the “function direction”) times “width of the interval” operation).
(think of the integral in terms of “area”; and this would be a height (in the “function direction”) times “width of the interval” operation).
What will be new is that we’ll consider 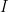 ‘s that might be much more complicated than a simple disjoint union of intervals. Well also show that if
‘s that might be much more complicated than a simple disjoint union of intervals. Well also show that if  and the union is disjoint and if
and the union is disjoint and if  is simple over both
is simple over both  and
and  then
then 


So, going back to our example functions 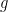 and
and  note that the “measure” of the rational numbers is zero as these can be covered by intervals whose lengths sum to arbitrarily small sums. So if we let
note that the “measure” of the rational numbers is zero as these can be covered by intervals whose lengths sum to arbitrarily small sums. So if we let 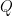 denote the rational numbers in
denote the rational numbers in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) and
and 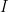 denote the irrationals, note that
denote the irrationals, note that 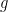 is a simple function over these two sets. Hence,
is a simple function over these two sets. Hence,
![\int_{[0,1]}g=](https://s0.wp.com/latex.php?latex=%5Cint_%7B%5B0%2C1%5D%7Dg%3D&bg=ffffff&fg=000000&s=0&c=20201002)


The second integral is more problematic; we’d have to break 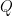 into a countable union of points whose coordinates have denominators 2, 3, 4,….and to prove a theorem about adding up a countable number of integrals
into a countable union of points whose coordinates have denominators 2, 3, 4,….and to prove a theorem about adding up a countable number of integrals
(e. g., forming a sequence). Getting to that point will take some work, as you can see.
Measure Theory.
Ok, we want to determine a “generalized length” of subsets of the real line, (subsets of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) for now) and these subsets can
for now) and these subsets can
be far more complicated than those which are finite disjoint collections of intervals (if you know what the Cantor “middle thirds” set is, you might
review that and if you don’t know what it is, look up “Cantor Set”; that will serve as a nice example of a complicated subset of the real line).
This is a main point of measure theory.
So, in abstract terms, what we are looking for is some sort of a map  from the collection of subsets of
from the collection of subsets of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) to the non-negative real numbers that serves as some sort of a length function. It might be a good time to stop and ask yourself: “what properties would we want this map (called a “measure”) to have?
to the non-negative real numbers that serves as some sort of a length function. It might be a good time to stop and ask yourself: “what properties would we want this map (called a “measure”) to have?
Here are some key properties:
1.![m([a,b])=b-a](https://s0.wp.com/latex.php?latex=m%28%5Ba%2Cb%5D%29%3Db-a&bg=ffffff&fg=000000&s=0&c=20201002) (and the same for open, and half open intervals). After all, this is supposed to be a length function. Of course,
(and the same for open, and half open intervals). After all, this is supposed to be a length function. Of course,
 .
.
2.  that is, measure should be “translation invariant” that is, if you translate a set
that is, measure should be “translation invariant” that is, if you translate a set  by adding the same constant to every element of
by adding the same constant to every element of 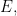 the translated set should have the same measure.
the translated set should have the same measure.
3.  (the measure of a single point and the empty set ought to be zero)
(the measure of a single point and the empty set ought to be zero)
4. If  then
then  and we’d like to have some additivity properties:
and we’d like to have some additivity properties:
5. Suppose  Then we’d want
Then we’d want  provided the left hand sum converges (of course, this convergence is absolute since all terms are positive; hence the order of the terms is of no consequence; this uses our calculus results).
provided the left hand sum converges (of course, this convergence is absolute since all terms are positive; hence the order of the terms is of no consequence; this uses our calculus results).
Of course, we are talking about a countable union; sums don’t make sense otherwise.
And, if the sets  are disjoint, we’d love to have
are disjoint, we’d love to have 
So how would we go about defining such a measure?
Here is one standard way: Every subset of the real line can be covered by a countable union of open intervals. (Note: if you said to yourself
anything about a Lindelof space, you have no business reading this article unless it is to critique it). So given a set 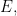 let
let  be a countable collection of open subintervals whose union contains
be a countable collection of open subintervals whose union contains  (that is, an open cover for
(that is, an open cover for  ). If
). If  is finite, call that the “length” of the cover of
is finite, call that the “length” of the cover of  Then consider the infimum of all lengths of covers of
Then consider the infimum of all lengths of covers of  (note: since
(note: since ![E \subset \lbrack 0,1]](https://s0.wp.com/latex.php?latex=E+%5Csubset+%5Clbrack+0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) , there exists a cover of length 1 so such an infimum exists). This infimum is
, there exists a cover of length 1 so such an infimum exists). This infimum is
called the measure of 
This definition of measure gives us most of what we want (1-5). Note: proving 1 is a bit trickier than it might first appear; it is immediate that
![m([a,b])\leq b-a.](https://s0.wp.com/latex.php?latex=m%28%5Ba%2Cb%5D%29%5Cleq+b-a.&bg=ffffff&fg=000000&s=0&c=20201002) To go the other way, one might use the fact that every open cover has a finite subcover (the Heinie-Borel Theorem from your analysis class) and induct on the number of open sets in your finite subcover). Features 2, 3, and 4 are pretty easy to demonstrate.
To go the other way, one might use the fact that every open cover has a finite subcover (the Heinie-Borel Theorem from your analysis class) and induct on the number of open sets in your finite subcover). Features 2, 3, and 4 are pretty easy to demonstrate.
5 (called “countable subadditivity”) Makes for an interesting exercise. I’ll sketch out a solution here:
Since each  has a measure, we’ll find a collection of open intervals
has a measure, we’ll find a collection of open intervals  that cover and, if
that cover and, if  denotes the length of the open interval, we can assume that
denotes the length of the open interval, we can assume that 
 Then note that
Then note that
 covers
covers  and
and


 for any
for any 
Hence  .
.
So what about the case where the  are disjoint; do we get equality?
are disjoint; do we get equality?
The answer is…well, NO…not for ALL subsets 
It will turn out that we will have to restrict our measure to certain subsets called “measurable sets”. The measurable sets form one large collection of subsets of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) that “work”. These sets will be those sets that have this condition:
that “work”. These sets will be those sets that have this condition:  (where
(where ![E^{\prime }=[0,1]-E](https://s0.wp.com/latex.php?latex=E%5E%7B%5Cprime+%7D%3D%5B0%2C1%5D-E&bg=ffffff&fg=000000&s=0&c=20201002) ; the set compliment of
; the set compliment of 
It isn’t obvious that this is the condition that we’ll need; this complement condition is called the Carathedory characterization.
Note: I am being a little bit sloppy here. Strictly speaking, I should use the concept of “outer measure” (that is, the “infimum of the sum of the lengths of the covers”) when talking about the Carathedory characterization and denote that by  and only use
and only use  when I am talking about the “measure” of the “measurable sets”; otherwise I would be using circular logic. But this isn’t a text book so I’ll abuse notation.
when I am talking about the “measure” of the “measurable sets”; otherwise I would be using circular logic. But this isn’t a text book so I’ll abuse notation.
Note: it is easy to establish that intervals and one point sets are measurable. To find other sets that are measurable, we’ll need to use
results from the algebra of sets;, sigma-algebras, etc.; the idea is to show that, say, the collection of measurable sets are closed with respect to countable unions, countable intersections, set complementation, etc.
This is one reason why set algebra topics are often covered in real analysis textbooks in the first sections or chapters. We’ll also show an example of a non-measurable set in a future post (2 dimensional versions of these come
into play in the Banach-Tarski “paradox”).
In the next section, we construct a non-measurable set.
,
, square roots, etc.
then it is reasonable to conclude that
. It is as if we want students to think that functions take integers to integers.
Now consider the following covering of the rational numbers:
. The length of each open interval is
. Of course there will be overlapping intervals but that isn’t important. What is important is that if one sums the lengths one gets
. So the rationals can be covered by a collection of open sets whose total length is less than or equal to 2.
and the total length is now less than or equal to
where
is any real number. Since there is no positive lower bound as to how small
can be, the set of rationals can be said to have measure zero.
