Student integral tricks…

Ok, classes ended last week and my brain is way out of math shape. Right now I am contemplating how to show that the complements of this object

and of the complement of the object depicted in figure 3, are NOT homeomorphic.

I can do this in this very specific case; I am interested in seeing what happens if the “tangle pattern” is changed. Are the complements of these two related objects *always* topologically different? I am reasonably sure yes, but my brain is rebelling at doing the hard work to nail it down.

Anyhow, finals are graded and I am usually treated to one unusual student trick. Here is one for the semester:

Now I was hoping that they would say at which case the integral is translated to: which is easy to do.

Now those wanting to do it a more difficult (but still sort of standard) way could do two repetitions of integration by parts with the first set up being and that works just fine.

But I did see this: (ok, there are some domain issues here but never mind that) and we end up with the transformed integral: which can be transformed to by elementary trig identities.

And yes, that leads to an answer of which, upon using the triangle

Gives you an answer that is exactly in the same form as the desired “rationalization substitution” answer. Yeah, I gave full credit despite the “domain issues” (in the original integral, it is possible for ).

What can I say?

I am going to celebrate this…

This marks the second summer in a row I got news that a paper of mine has been accepted for publication. Last year, it was the College Mathematics Journal; this year it is the Journal of Knot Theory and its Ramifications.

Sure, that is a big “yawn”, “so what”, or “is that all?” for faculty at Division I research universities. But I teach at a 11-12 hour load institution which also has committee requirements.

And, to be blunt: I got my Ph. D. in 1991 and has a somewhat long slump in publication; I was beginning to wonder if my intellect had atrophied with time.

Ok, it has, in the sense that I don’t pick up material as quickly as I once did. But to counter that, the years of teaching across the curriculum (from business calculus to operations research to numerical analysis to differential equations) and the years of attending talks and attempting to learn new things has given me a bit more perspective. I make fewer “hidden assumptions” now.

So, I am going to celebrate this one…and then get back to work on spin-off ideas.

The Quadratic Formula: case study in misunderstanding its meaning (and a moral)

I admit that I never dreamed that something as innocent as this picture (a friend tagged me on Facebook) would lead to a sort-of heated argument.

Of course this is the famous quadratic formula; it gives the roots to the following equation: with complex numbers and interpreted as the principle solution to . In fact this works in any field in which the square root is defined.
This formula is just a trivial consequence of completing the square: assume that 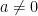then
which implies which implies which implies which implies which is the formula.

But one of my friend’s “Facebook Friends” said:

I’ve never actually used the quadratic equation, i just relied on algebraic reasoning

That is a curious statement; my friend remarked that the quadratic formula WAS “algebraic reasoning.” I was curious as to what the comment meant so I posted

Ok, solve 2x^2 + 13x – 17 = 0 without using the quadratic formula OR completing the square (the two are actually the same thing).”

Then came the following response:

when you say 2x^2, do you mean (2x)^2? if so then it is one. it really is easy. you are talking to someone who took ap classes from an MIT grad without using a calculator. and jason, the quadratic formula is an example of algebraic reasoning, which is to say that there are other methods. I was not trying to imply that the quadratic formula is different from algebraic reasoning. math is the language of logic, so i usually relied on my own means to find the answer, although my means can be convoluted at times.

Evidently this individual didn’t understand the significance of my response. This is evident later:

“You really should reserve that for yourself. If it is a quadratic equation, it will almost always have more than one answer, which is outlined by the +/- part of the quadratic equation. Is 1 a possible answer? yes. Is it the only answer? no. I am referring to the the equation i provided btw. Did I assert that 1 was the ONLY answer? no.”
[…]
“I know, that is why i said it wasnt the one I was referring to the whole time. Why else would I ask to clarify? I already know that if I were to go with 2x^2, it would produce an answer with a decimal. That is because if you follow the quadratic equation you will notice that the number in the square root is 305, and the root of the 305 is pretty messy.”

See where the confusion is? Evidently he (yes, the friend and his Facebook friend is a male) did not understand that, while the quadratic formula (or the completing the square process) yields ALL possible solutions for every true quadratic () that in no way means that one can’t, at times, guess a solution or, at times, find an easy factorization. So if you want to solve the general quadratic and find all solutions, you need this formula or the completing the square process.

Of course, in the complex coefficients case, the answer is frequently ugly.

Side notes: there is a formula for the solution to a cubic (very messy) and for the degree 4 polynomial. However, it is impossible to find a general formula to solve the degree 5 polynomial; this is a reason to learn some Galois Theory from abstract algebra!

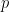The other fields: in general the quadratic cannot be solved if the field is, say, an integer of odd prime order, unless one extends the field by adjoining where is the prime in question. This is a good reason to learn some number theory.

Moral
Often, students will put the time and effort into understanding a concept if they know WHY it is important. However, they don’t always appreciate what a formula like the quadratic does. One doesn’t always have to use it, but it
1. Provides a method of obtaining ALL solutions that is guaranteed to work in every case (where )
2. Proves that, in fact, the solutions always exist and what kind they are (real or complex).

These points are not obvious to every beginner, even some who consider themselves to be “bright” and talented. Such self perceptions are the topic of a different post.

Issues in the News…

First of all, I’d like to make it clear that I am unqualified to talk about teaching mathematics at the junior high and high school level. I am qualified to make comments on what sorts of skills the students bring with them to college.

But I am interested in issues affecting mathematics education and so will mention a couple of them.

1. California is moving away from having all 8’th graders take “algebra 1”. Note: I was in 8’th grade from 1972-1973. Our school was undergoing an experiment to see if 8’th graders could learn algebra 1. Being new to the school, I was put into the regular math class, but was quickly switched into the lone section of algebra 1. The point: it wasn’t considered “standard for everyone.”

My “off the cuff” remarks: I know that students mature at different rates and wonder if most are ready for the challenge by the 8’th grade. I also wonder about “regression to the mean” effects of having everyone take algebra 1; does that force the teacher to water down the course?

2. What would college students want to tell their high school teachers?

By Drew Appleby

I read Epstein School head Stan Beiner’s guest column on what kids really need to know for college with great interest because one of the main goals of my 40-years as a college professor was to help my students make a successful transition from high school to college.

I taught thousands of freshmen in Introductory Psychology classes and Freshman Learning Communities, and I was constantly amazed by how many of them suffered from a severe case of “culture shock” when they moved from high school to college.

I used one of my assignments to identify these cultural differences by asking my students to create suggestions they would like to give their former high school teachers to help them better prepare their students for college. A content analysis of the results produced the following six suggestion summaries.

The underlying theme in all these suggestions is that my students firmly believed they would have been better prepared for college if their high school teachers had provided them with more opportunities to behave in the responsible ways that are required for success in higher education […]

You can surf to the article to read the suggestions. They are not surprising; they boil down to “be harder on us and hold us accountable.” (duh). But what is more interesting, to me, is some of the comments left by the high school teachers:

“I have tried to hold students accountable, give them an assignment with a due date and expect it turned in. When I gave them failing grades, I was told my teaching was flawed and needed professional development. The idea that the students were the problem is/was anathema to the administration.”

“hahahaha!! Hold the kids responsible and you will get into trouble! I worked at one school where we had to submit a written “game plan” of what WE were going to do to help failing students. Most teachers just passed them…it was easier. See what SGA teacher wrote earlier….that is the reality of most high school teachers.”

“Pressure on taechers from parents and administrators to “cut the kid a break” is intense! Go along to get along. That’s the philosophy of public education in Georgia.”

“It was the same when I was in college during the 80’s. Hindsight makes you wished you would have pushed yourself harder. Students and parents need to look at themselves for making excuses while in high school. One thing you forget. College is a choice, high school is not. the College mindset is do what is asked or find yourself another career path. High school, do it or not, there is a seat in the class for you tomorrow. It is harder to commit to anything, student or adult, if the rewards or consequences are superficial. Making you attend school has it advantages for society and it disadvantages.”

My two cents: it appears to me that too many of the high schools are adopting “the customer is always right” attitude with the student and their parents being “the customer”. I think that is the wrong approach. The “customer” is society, as a whole. After all, public schools are funded by everyone’s tax dollars, and not just the tax dollars of those who have kids attending the school. Sometimes, educating the student means telling them things that they don’t want to hear, making them do things that they don’t want to do, and standing up to the helicopter parents. But, who will stand up for the teachers when they do this?

Note: if you google “education then and now” (search for images) you’ll find the above cartoons translated into different languages. Evidently, the US isn’t alone.

Statistics Education
Attaining statistical literacy can be hard work. But this is work that has a large pay off.
Here is an editorial by David Brooks about how statistics can help you “unlearn” the stuff that “you know is true”, but isn’t.

This New England Journal of Medicine article takes a look at well known “factoids” about obesity, and how many of them don’t stand up to statistical scrutiny. (note: the article is behind a paywall, but if you are university faculty, you probably have access to the article via your library.

And of course, there was the 2012 general election. The pundits just “knew” that the election was going to be close; those who were statistically literate knew otherwise.

One challenge of teaching “brief calculus” (“business calculus”, “applied calculus”, etc.)

Today’s exam covered elementary integrals and partial derivatives; in our course we usually mention two variable functions and show how to calculate some “easy” partial derivatives.

So today’s exam saw a D/F student show up late (as usual); keep in mind this is an 8 am class (no class prior to it). He, as usual, got little or nothing correct. Of course we had the usual , etc.

But there was this too: note that we had barely discussed partial derivatives and how to calculate them “by the formula”. But I did give the following bonus question: “is it possible to have a function where and ? Yes, this is a common question in multivariable calculus (e. g., “is this vector field conservative?”) but remember this is a “brief calculus” course.

A few students took the challenge; some computed and noted that the two functions cannot be made to match (I didn’t expect them to recognize that functions of one variable alone represents constants of integration). Some took the second partials and noted and that these don’t match. Again, this was NOT a problem that we practiced.

Another instance: given the ideal gas law I challenged them to show and someone got it!

Bottom line: in one course, we have some bright, interested students who enjoy thinking and we have some who either don’t or can’t. This makes teaching difficult; if one tries to “teach to the mean” one is teaching to the empty set. It is almost: either bore half the class, or blow away half the class.

Mathfest Day III

I only attended the major talks; the first one was by Richard Kenyon. The material, while interesting, flew by a little quickly (though it wouldn’t have for someone who researches full time). The main idea: piecewise approximation to smooth objects is extremely useful, not only topologically but also geometrically (example)

Something especially interesting to me: when trying to approximate certain smooth surfaces, the starting approximation doesn’t matter that much; there are many different piecewise linear sequences that converge to the same surface (not a surprise). There is much more there; this is a lecture I’d like to see again (if it gets posted).

The next one was the third Bernd Sturmfels; this was a continuation of his “algebraic geometry’s usefulness in optimization” series. One big idea: we know how to optimize a linear function on a polygon (e. g., simplex method). It turns out that we can sometimes speed up the process by the “central curve” method; the idea is to use algebraic geometry to do an optimization problem on the constraint plus a term involving logs: form where is the cost function. There is much more there.

The last talk was by an Ivy League professor; it was called “putting topology to work”. On one hand, it was great in the sense that there were many interesting applications. He then asked a sensible question: “how do we teach the essentials of this topology to engineers”?

His solution: revise the undergraduate curriculum so that…well…undergraduates had algebraic topology (or at least homological algebra) in their…linear algebra course. 🙂 It must be nice to teach Ivy league caliber undergraduates. 🙂

The elephant in the room: NO ONE seemed to ask the question: “do the students in our classrooms have the ability to learn this stuff to begin with?”

Do you really think that a class full of students with ACTs in the 22-26 range will be able to EVER handle the advanced stuff, no matter how well it is taught?

Teaching Calculus to Biology Students

Currently, I am teaching the second semester of “brief calculus” (or “applied calculus” or “business calculus”) and have a class that has a high percentage of motivated students.

Most are biology majors; a few are chemistry majors.

What I found: these students will work to understand the material but don’t catch on nearly as quickly as, say, engineers. One reason why: I began to understand that engineers spend time in their classes talking about ideas in mathematical language; they throw around trig functions, exponential functions, Taylor series, derivatives and differential equations in their respective classes. Hence when they walked into my differential equations class, their “math brains” have been “warmed up”, so to speak.

On the other hand, this isn’t true for many of my biology students; the language of the class is different from what they are used to.

But these are NOT dumb people; they will work to understand the concepts and eventually understand them.

But it takes a bit more time for them; they need more examples and some patience.

The “equals” sign: identities, equations to be solved and all that…

Here is the sort of thing that got me thinking about this topic: a colleague had a student complain about how one of her quiz problems was scored. The problem stated: “show that “. She was offended that her saying “” wasn’t enough to receive credit and would NOT take his word for it. In fact, she took this to the student ombudsman!!!

But that raised the question: “what do we mean when we tell our students ““?

Of course, there are some central issues here. The first issues is that our “sure of herself” student thought that “” meant that this relation is NEVER true for any choice of , which of course, is false (e. g. let and .) In fact, is the logical negation of the statement ; the latter means that “this statement is true for ALL and its negation means “there is at least one choice of for which the statement is not true. “Equal” and “not equal” are not symmetric states when it comes identities, which can be thought of as elements in the vector space of functions.

So, means that and are not equal in function space, though they might evaluate to the same number for certain choices in the domain.

So, what is the big deal?

Well, what about equations such as or ?
These are NOT equalities in the space of functions; the first means “what values in the domain does take given and the second asks one to find the inverse image of 0 for the operator where the domain is the set of all, say, twice differentiable functions.

But, but…would the average undergraduate student understand ANY of this? My experience tells me “no”; hence I intentionally allow for this vagueness and only address it as I need to.

Teaching Mathematics in this era: The Helicopter Parent

Mathematics Education
I was somewhat taken aback at this Daily Kos diary:

I was asked how my daughter is doing. She has 16 credits to go to her bachelor’s degree but it might as well be 2 more years. She’s up in Michigan licking her math wounds. She’s trying to gear up for what she has to do to complete her degree. She had her math ass kicked this last term – again. My daughter, the high school mathlete can’t hack collegiate Calculus II, Differential Equations or Multivariate Analysis (aka Calculus III on steroids) well enough to get a 73.5% or higher which is a requirement for her Physics B.A. degree. She can get 70% and 71%, but not the 73.5% deemed necessary. I mentioned that our current strategy is to find an instructor who’s actually teaching these classes in another school in town (we have 6 major colleges and universities in town to choose from) and transfer in the credits so she can get her degree.

Well, that statement set the mouse amongst the pooties.

How could I say that! Was I saying the instructors weren’t teaching! (That would be sacrilegious in this group.) What’s strange is that I wasn’t criticizing Chibi’s elementary, middle or high school math experience. Her high school math classes were the last classes where actual math instruction occurred. We complain about education and math education in particular, but Chibi got decent math education through to her Senior year in high school. She did well there. It’s university math outside the physics department that’s giving her trouble. She aces all her Physics & Calculus classes that require her to calculate vortexes, how moisture flows through tail pipes, predicting the sizes of hail stones or whatever; these aren’t difficult for her. It’s the math for math’s sake classes, where there’s a bare equation with no real world application or context for solving it that kicks her butt. The lack of practical application simply stymies her mathlete abilities. […]

One thing is for certain, as long as we continue to teach collegiate math using 100 year old methods, the U.S. math competencies will remain where they are.

So do you get this: his daughter did well in high school mathematics but didn’t do well in college mathematics, so it must be the fault of the mathematics professors….ALL of them. Then he blames our position with respect to the world in mathematics education on the university mathematics faculty.

Let’s examine this for a bit:

The disappointing performance of U.S. teenagers in math and science on an international exam, in scores released yesterday, has sparked calls for improvement in public schools to help the country keep pace in the global economy.

The scores from the 2006 Program for International Student Assessment showed that U.S. 15-year-olds trailed their peers from many industrialized countries. The average science score of U.S. students lagged behind those in 16 of 30 countries in the Organization for Economic Cooperation and Development, a Paris-based group that represents the world’s richest countries. The U.S. students were further behind in math, trailing counterparts in 23 countries.

The gap is already there by the time the kids are 15 years old….and exactly how is this the fault of university mathematics faculty?
Remember, his complaint was that his daughter got good grades in high school mathematics but didn’t get them in college mathematics…in several classes. What was the constant there? It was his daughter, of course.

In short, this person makes a sweeping claim based on the lack of success of HIS KID. THIS is part of the “helicopter parent” era.

I’ll add a few thoughts from my experience: in high school, I made A’s in foreign language but had to work to earn a C in my junior level class in college. The professor was excellent; the material was just difficult for me. Even in mathematics: I did well in analysis, algebra, topology and ok in complex variables. I struggled badly in numerical analysis. Yes, my numerical analysis professor…was quite good and I said so on the student evaluations. I just didn’t do well IN THAT CLASS. It just took a long time for that material to make sense to me.

I am not saying that there aren’t some horrible mathematics instructors: there are. That is unfortunate, but there are there. But that is not an excuse for repeated poor performance in classes.

Upshot: there are some parents who will never admit that their student really isn’t that good; the fault will always lie elsewhere.

Note: I am NOT saying that not doing well in mathematics makes anyone a failure. For example: my step son took the multi-year path to get through the required calculus sequence required by his computer science program. He got his degree and is now earning (at least) triple my salary in the database industry.

The founder of Jetblue Airlines didn’t do well in mathematics.

A possible way to explain the contrapositive

Mathematics Education

This post at Schneier’s security blog is very interesting. The gist of the post is this: do you remember the simple logical rule: “P implies Q” is equivalent to “not Q implies not P”. Example: if you have the statement “green apples are sour” means that if you bite an apple and it isn’t sour, then it can’t be green. In my opinion, there is nothing hard about this. We use this principle all of the time in mathematics! As an example, consider how we prove that there is no largest prime: Suppose that there was a largest prime with the previous (finite) primes indexed. Now form the number Now cannot be prime because it is bigger than So it is composite and therefore has prime factors. But this is impossible because can never divide because it divides . QED.

The whole structure of the proof by contradiction is the principle that “p implies q” is equivalent “not q implies not p”. Here the q is “there is no biggest prime” and the “suppose there IS a biggest prime” is the “not q” which ended up implying “not p” where p is the true statement that and are relatively prime.
No mathematician would have a problem using that bit of logic.

But evidently mathematicians are in the minority.

Consider this experiment:

Consider the Wason selection task. Subjects are presented with four cards next to each other on a table. Each card represents a person, with each side listing some statement about that person. The subject is then given a general rule and asked which cards he would have to turn over to ensure that the four people satisfied that rule. For example, the general rule might be, “If a person travels to Boston, then he or she takes a plane.” The four cards might correspond to travelers and have a destination on one side and a mode of transport on the other. On the side facing the subject, they read: “went to Boston,” “went to New York,” “took a plane,” and “took a car.”

So, which card needs to be turned over? Of course, the card has to be “went to Boston” because there is nothing in the rule about going to New York, there is nothing that says that Boston is the only place you can fly to, and turning over the “car card” might reveal “New York” as a destination. Evidently, this problem is hard for most people.
But here is where this gets interesting: if the exact same logical problem is phrased as a “fairness rule”; say “for you to play in a game, you must attend practice” then the problem because very easy for people to solve! Schneier concludes:

Our brains are specially designed to deal with cheating in social exchanges. The evolutionary psychology explanation is that we evolved brain heuristics for the social problems that our prehistoric ancestors had to deal with. Once humans became good at cheating, they then had to become good at detecting cheating — otherwise, the social group would fall apart.

So, maybe I can use the fact that people seem to understand this rule in this setting when it comes to teaching this point of logic?