J. H. Conway, Terry Tao and avoiding work

The mainstream media recently had some excellent articles on two mathematical giants:

John Conway and Terrance Tao. I’ve never met Terry Tao though I do read (or try to follow) his blog.

I did meet John Conway when he visited the University of Texas. He is a friend of my dissertation advisor and gave some talks on knot diagram colorings.

I had a private conversation with him at a party, and he gave me some ideas which resulted in three papers for me! Here is one of them.

Yes, I am avoiding studying a book on the theory of interest; I am teaching that course this fall and need to get ahead of the game.

Unfortunately, when I don’t teach, my use of time becomes undisciplined.

Trolled by Newton’s Law of Cooling…

From a humor website: there is a Facebook account called “customer service” who trolls customers making complaints. Though that isn’t a topic here, it is interesting to see Newton’s Cooling Law get mentioned:

Knowledge that can’t be communicated is worthless

In the past, I’ve passed out this cartoon to my students. Too many times, I’ve heard “I understand how to do the problem, but I can’t do the problem on the exam.”

Well, I suppose that is a bit like saying:

“I know how to swim, but when I jump in the pool, I drown.”

“I know how to fly the plane, but when I try, I crash.”

Embarrassing gaps in my mathematical knowledge

Yes, mathematics is a huge, huge subject and no one knows everything. And, when I was a graduate student, I could only focus on 1-2 advanced courses at a time, and when I was working on my thesis, I almost had a “blinders on” approach to finishing that thing up. I think that I had to do that, given my intellectual limitations.

So, even in “my area”, my knowledge outside of a very narrow area was weak at best.

Add to this: 20+ years of teaching 3 courses per semester; I’ve even forgotten some of what I once knew well, though in return, I’ve picked up elementary knowledge in disciplines that I didn’t know before.

But, I have many gaps in my own “area”. One of these is in the area of hyperbolic geometry and the geometry of knot complements (think of this way: take a smooth simple closed curve in , add a point at infinity to get (a compact space), now take a solid torus product neighborhood of the knot (“thicken” the knot up into a sort of “rope”) then remove this “rope” from . What you have left over is a “knot complement” manifold.

Now these knot complements fall into one of 3 different types: they are torus knot complements (the knot can live on the “skin” of a torus),

satellite knot complements (the knot can live inside the solid torus that is the product neighborhood of a different, mathematically inequivalent knot,

or the knot complement is “hyperbolic”; it can be given a hyperbolic structure. At least for “most” knots of small “crossing number” (roughly: how many crossings the knot diagram has), are hyperbolic knots.

So it turns out that the complement of such knots can be filled with “horoballs”; roughly speaking, these are the interior of spheres which are “tangent to infinity”; infinity is the “missing stuff” that was removed when the knot was removed from 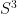. And, I really never understood what was going on at all.

I suppose that one can view the boundary of these balls (called “horospheres”) as one would view, say, the level planes in ; those planes become spheres when the point at infinity is added. This is a horoball packing of the complement of the figure 8 knot; missing is the horosphere at which can be thought of as a plane.

But the internet is a wonderful thing, and I found a lecture based on the work of Anastasiia Tsvietkova and Morwen Thistlethwaite (who generated the horoball packing photo above) and I’ll be trying to wrap my head around this.