The potential harm in using outliers as examples…..

I think that this is common in this day and age: I have some students who are struggling in our “elementary conceptual calculus” course. They come to class, but work a large number of hours at a job in order to make ends meet. So…they are often left with very little time to study.

And yes, IN THIS COURSE, most of the students need to study quite a bit in order to have a chance at even a “C”.

In short: most students need to have a certain number of hours in order to sleep and to study..in addition to making the classes and their part time jobs.

Now, some might say that this is nonsense.

I remember a professor I had at the Naval Academy. He said that when he was an undergraduate he studied very little for his math classes as he paid his own way through school by waiting tables. He made up for it by PAYING ATTENTION IN CLASS.

That is well and good…..but then remember that he had an earned Ph.D. in mathematics from MIT.

Most of us don’t have that type of natural ability.

Yes, Mohammed Ali could break the conventional rules of boxing (dangle his arms, lean away from punches):

But most, including most other professional boxers, don’t have that kind of ability.

Yes, there are people who can run a 2:15 marathon on 35 miles a week of training:

Following the 1976 trials he trained by running 35 miles per week and ran “a 2:14:37 for second place at the Nike-Oregon Track Club Marathon in Eugene in 1978. After that, he ran 2:15:23 for 15th place in the Boston Marathon in 1979.”

But most of us aren’t that gifted (this was Tony Sandoval, cowinner of the 1980 US Olympic Trials Marathon)

Yes, some can make a successful film while being stoned on marijuana, but most of us aren’t as talented as the Beatles.

The list can go on and on. The bottom line: you can gain inspiration from the incredibly successful, but you won’t be able to get away with taking the short cuts that many of them got away with. Neither you nor I are outliers.

Why don’t you people use NUMBERS instead of letters?

Yes, some people have asked me this: “why all of the letters? Why don’t you use NUMBERS?”.

If I am in a patient mood I might say something like: “ok, suppose you want to be able to program a computer to compute a tax on an order? Well, you’d need the item ordered, the price of the item ordered, how many of each item ordered and the applicable tax, right?

Well, there is a “slot” in the order form for each of those, and the “letters” we use stand for such slots.”

Usually, these questions come from those who haven’t had the benefit of an education.

I expect better from our political leaders, and from time to time I am disappointed in them:

Ignoring pleas from business leaders, the Senate Education Committee voted 6-3 along party lines Thursday to bar Arizona from implementing the Common Core standards the state adopted four years ago.

Sen. Al Melvin, R-Tucson, who championed SB 1310, said he believes the concept of some nationally recognized standards started out as a “pretty admirable pursuit by the private sector and governors.”

“It got hijacked by Washington, by the federal government,” said Melvin, a candidate for governor, and “as a conservative Reagan Republican I’m suspect about the U.S. Department of Education in general, but also any standards that are coming out of that department.”

Melvin’s comments led Sen. David Bradley, D-Tucson, to ask him whether he’s actually read the Common Core standards, which have been adopted by 45 states.

“I’ve been exposed to them,” Melvin responded.

Pressed by Bradley for specifics, Melvin said he understands “some of the reading material is borderline pornographic.” And he said the program uses “fuzzy math,” substituting letters for numbers in some examples.

No, this isn’t satire. I wish that it were.

Note while there ARE legitimate criticisms of Common Core; using “letters for numbers” isn’t one of them.

Note: the above link was brought to my attention by someone on Facebook.

A real valued function that is differentiable at an isolated point

A friend of mine is covering the Cauchy-Riemann equations in his complex variables class and wondered if there is a real variable function that is differentiable at precisely one point.

The answer is “yes”, of course, but the example I could whip up on the spot is rather pathological.

Here is one example:

Let be defined as follows:

That is, if is irrational or zero, and is if is rational and where .

Now calculate

Let be given and choose a positive integer so that . Let . Now if and is irrational, then .

Now the fun starts: if is rational, then and .

We looked at the right hand limit; the left hand limit works in the same manner.

Hence the derivative of exists at and is equal to zero. But zero is the only place where this function is even continuous because for any open interval , .

Recreational math problem with a spreadsheet

I saw this on Facebook:

Yes, I know, there are different formulas that work. So suppose we want ” 3 + 5″ to “equal” -28. What we want is the first digests (the constant coefficient upwards) to be the sum of the numbers, and the “leading” digits to be “a-b” with a correct sign; that is: a “+” b = (a-b, a+b) with the comma removed so as to make a single integer (the inputs are integers).

So the “cute” problem: get a spread sheet to do this.

To get full credit: you must get the correct answer for both a greater than b and a “less than” b.

Dunning-Kruger effect in lower division courses

If you don’t know what the Dunning-Kruger effect is, go here. In a nutshell: it takes a bit of intelligence/competence to recognize one’s own incompetence.

THAT is why I often dread handing exams back in off-semester “faux calculus” courses (frequently called “brief calculus” or “business calculus”).

The population for the “off semester”: usually students who did poorly in our placement exams and had to start with “college” algebra, or people who have already flunked the course at least once, as well as people who simply hate math.

That many have little natural ability doesn’t bother me. That they struggle to understand that “a number” might be zero doesn’t bother me that much (context: I told them that ALWAYS fails to exist if both limits exist and and .)

What bothers me: some won’t accept the following: if THEY think that they are right and I tell them that they are wrong, there is very high probability that I am right. Too many just refuse to even entertain this idea, no matter how poor their record in mathematics is.

Of course, other disciplines have it worse….so this is just a whine about teaching the very bad students in what amounts to a remedial course.

Aitken acceleration: another “easy” example for the students

In a previous post I showed some spreadsheet data to demonstrate the Aitken acceleration process. Here, I’ll go through an example where a sequence converges linearly: let where . We use the form (I am too lazy to use the traditional “p-hat” notation). First, note that the denominator works out to

The numerator is a tiny bit more work: the terms cancel and as far as the rest:

which simplifies to a term involving and one that doesn’t. Here is the term involving :

which, of course, is just times the denominator.

Now the terms not involving :

So our fraction is merely

This can be rearranged to

Clearly as goes to infinity, the error goes to zero very quickly. It might be instructive to look at the ratio of the errors for and :

This ratio is

Note that in the right hand factor: both squared factors are fixed and the coefficients go to infinity as goes to infinity. If one multiplies out, one obtains:

. In the limit, the first term decreases to and the second goes to infinity.

Hence the errors in the accelerated sequence are smaller.

Demonstrating Aitken’s sequence acceleration

Right now, we are studying the various root finding algorithms in Numerical Analysis (bisection, Newton’s, etc.)

Such algorithms yield a sequence of numbers, which (hopefully) converge to a solution: .

Of course, each point in the sequence is obtained by calculations and, if there were a way to combine these points so as to obtain a sequence that converges faster (while not adding much to the computation complexity), there is some benefit. And yes, it is possible to use the sequence points, do the series manipulation and use the manipulated points in the root finding algorithm itself (e. g. Steffensen’s method).

In this post, I’ll talk about Aitken’s method and how one can cook up examples that not only show that the method can work but give the students some intuition as to why it might work.

I’ll provide just a bit of background in the event that the general reader comes across this.

Let . If we have ( is positive, of course) we say that the convergence is LINEAR if and the inequality must be strict. If then we say that convergence is quadratic (regardless of .)

To see the reason for the terminology, just multiply both sides of the “defining equation” by the denominator. In the linear case : so one can think: “get new approximation by multiplying the old approximation by some constant less than one”. For example: exhibits linear convergence to 0; that is a decent way to think about it.

Now (in the linear convergence case anyway), suppose you think of your approximation having an error that shrinks with iteration but shrinks in the following way: the n’th iteration looks like where are constants strictly between 0 and 1. Of course, as goes to infinity, approaches the limit as the error terms die away.

Aitken’s method is this: let’s denote a new sequence by . (I am not using the traditional P-hat out of laziness) Then . To see how this formula is obtained, check out these excellent course notes. Or the Wiki article is pretty good.

Look at the numerator of what is being subtracted off: if we have the terms written (very roughly) as and if, say, is much larger than , then will be closer to than is to , hence more of this error will be subtracted away.

Yes, I know that his is simple-minded, but it “gets the spirit” of the process. I’ve set up some spreadsheets with “cooked” sequences linearly converging to zero and showed how the Aitken process works there. Note: the spreadsheet round off errors start occurring at the range; you can see that here.

(click to see the larger image)

To see an abstract example where where , go to the next post in this series.

Numerical methods class: round off error using geometric series and spreadsheets…

Of course computers store numbers in binary; that is numbers are represented by where each (of course the first coefficient is 1).

We should probably “warm up” by showing some binary expansions. First: someone might ask “how do I know that a number even HAS a binary expansion? The reason: the dyatic rationals are dense in the number line. So just consider a set of nested partitions of the number line, where each partition in the family has width and it isn’t hard to see a sequence that converges to a given number. That sequence leads to the binary expansion.

Example: What is the binary expansion for 10.25?

Answer: Break 10.25 down into 10 + 0.25.

so the “integer part” of the binary expansion is .

Now for the “faction part”: in binary.

Hence in base 10 in binary.

So what about something harder? Integers are easy, so lets look at where each .

Clearly since is greater than . Now so multiply both sides of by 4 to obtain

Now subtract 1 from both sides and get Here so multiply both sides by 2 and subtract 1 and get

Note that we are back where we started. The implication is that and so the base 2 decimal expansion for is

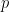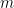Of course there is nothing special about ; a moment’s thought reveals that if one starts with where is less than , the process stops (we arrive at zero on the left hand side) or we return to some other where is less than ; since there are only a finite number of 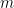we have to arrive at a previous fraction eventually (pigeonhole principle). So every rational number has a terminating or repeating binary decimal expansion.

Now it might be fun to check that we did the expansion correctly; the geometric series formula will help:

Now about how the computer stores a number: a typical storage scheme is what I call the 1-11-52 scheme. There are 64 bits used for the number. The first is for positive or negative. The next 11 bits are for the exponent. Now so technically the exponent could be as large as . But we want to be able to store small numbers as well, so is subtracted from this number so we could get exponents that range from to . Also remember these are exponents for base 2.

This leaves 52 digits for the mantissa; that is all the computer can store. This is the place where one can look at round off error.

Let’s see two examples:

10.25 is equal to . The first bit is a 0 because the number is positive. The exponent is 3 and so is represented by which is . Now the mantissa is assumed to start with 1 every time; hence we get 0100100000000000000000000000000000000000000000000000.

So, let’s look at the example. The first digit is 0 since the number is positive. We write the binary expansion as: . The exponent is which is stored as . Now the fun starts: we need an infinite number of bits for an exact representation but we have 52. is what is repeated so we can repeat this 51 times plus the next 0. So the number that serves as a proxy for is really

Ok, about spreadsheets:

Of course, it is difficult to use base 2 directly to demonstrate round off error, so many texts use regular decimals and instruct the students to perform calculations using “n-digit rounding” and “n-digit chopping” to show how errors can build up with iterated operations.

One common example: use the quadratic formula to find the roots of a quadratic equation. Of course the standard formula for the roots of is and there is an alternate formula that leads to less round off error in the case when the “alternative formula” denominator has large magnitude.

Now the computations, when done by hand, can be tedious and more of an exercise in repeated calculator button punching than anything else.

But a spreadsheet can help, provided one can find a way to use the “ROUND(N, M)” command and the “TRUNC(N, M)” commands to good use. In each case, N is the number to be rounded or truncated and M is the decimal place.

A brief review of these commands: the ROUND command takes a decimal and rounds to the nearest place; the TRUNC truncates the decimal to the nearest place.
The key: M can be any integer; positive, negative or zero .

Examples: TRUNC(1234.5678, 2) = 1234.56, TRUNC(1234.5678, -1) = 1230, ROUND(1234.5678, 3) = 1234.569, ROUND(1234.5678, -2) = 1200.

Formally: if one lets for all and if then TRUNC(x, M) =

So if M is negative, this process stops at a positive power of 10.

That observation is the key to getting the spread sheet to round or truncate to a desired number of significant digits.

Recall that the base 10 log picks of the highest power of 10 that appears in a number; for example So let’s exploit that: we can modify our commands as follows:

for TRUNC we can use TRUNC(N, M -1 – INT(log10(abs(N)))) and for ROUND we can use ROUND(N, M -1 – INT(log10(abs(N)))). Subtracting the 1 and the integer part of the base 10 log moves the “start point” of the truncation or the rounding to the left of the decimal and M moves the truncation point back to the right to the proper place.

Of course, this can be cumbersome to type over and over again, so I recommend putting the properly typed formula in some “out of the way” cell and using “cut and paste” to paste the formula in the proper location for the formula.

Here is an example:
This spread sheet shows the “4 digit rounding” calculation for the roots of the quadratics and respectively.

(click for a larger view).

Note that one has to make a cell for EVERY calculation because we have to use 4 digit arithmetic at EACH step. Note also the formula pasted as test in the upper right hand cell.

One can cut an paste as a cell formula as shown below:

Here one uses cell references as input values.

Here is another example:

Note the reference to the previous cells.