This might seem like a strange topic but right now our topology class is studying compact metric spaces. One of the more famous of these is the “Cantor set” or “Cantor space”. I discussed the basics of these here.
Now if you know the relationship between a countable product of two point discrete spaces (in the product topology) and Cantor spaces/Cantor Sets, this post is probably too elementary for you.
Construction: start with a two point set  and give it the discrete topology. The reason for choosing 0 and 2 to represent the elements will become clear later. Of course,
and give it the discrete topology. The reason for choosing 0 and 2 to represent the elements will become clear later. Of course,  is a compact metric space (with the discrete metric:
is a compact metric space (with the discrete metric:  if
if  .
.
Now consider the infinite product of such spaces with the product topology:  where each
where each  is homeomorphic to
is homeomorphic to  . It follows from the Tychonoff Theorem that
. It follows from the Tychonoff Theorem that  is compact, though we can prove this directly: Let
is compact, though we can prove this directly: Let  be any open cover for
be any open cover for  . Then choose an arbitrary
. Then choose an arbitrary  from this open cover; because we are using the product topology
from this open cover; because we are using the product topology  where each
where each  is a one or two point set. This means that the cardinality of
is a one or two point set. This means that the cardinality of  is at most
is at most  which requires at most
which requires at most  elements of the open cover to cover.
elements of the open cover to cover.
Now let’s examine some properties.
Clearly the space is Hausdorff ( ) and uncountable.
) and uncountable.
1. Every point of  is a limit point of
is a limit point of  . To see this: denote
. To see this: denote  by the sequence
by the sequence  where
where  . Then any open set containing
. Then any open set containing  is
is  and contains ALL points
and contains ALL points  where
where  for
for  . So all points of
. So all points of  are accumulation points of
are accumulation points of  ; in fact they are condensation points (or perfect limit points ).
; in fact they are condensation points (or perfect limit points ).
(refresher: accumulation points are those for which every open neighborhood contains an infinite number of points of the set in question; condensation points contain an uncountable number of points, and perfect limit points are those for which every open neighborhood contains as many points as the set in question has (same cardinality).
2.  is totally disconnected (the components are one point sets). Here is how we will show this: given
is totally disconnected (the components are one point sets). Here is how we will show this: given  there exists disjoint open sets
there exists disjoint open sets  . Proof of claim: if
. Proof of claim: if  there exists a first coordinate
there exists a first coordinate 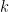 for which
for which  (that is, a first
(that is, a first 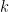 for which the canonical projection maps disagree (
for which the canonical projection maps disagree ( ). Then
). Then
 ,
,

are the required disjoint open sets whose union is all of  .
.
3.  is countable, as basis elements for open sets consist of finite sequences of 0’s and 2’s followed by an infinite product of
is countable, as basis elements for open sets consist of finite sequences of 0’s and 2’s followed by an infinite product of  .
.
4.  is metrizable as well;
is metrizable as well;  . Note that is metric is well defined. Suppose
. Note that is metric is well defined. Suppose  . Then there is a first
. Then there is a first  . Then note
. Then note

which is impossible.
5. By construction  is uncountable, though this follows from the fact that
is uncountable, though this follows from the fact that  is compact, Haudorff and dense in itself.
is compact, Haudorff and dense in itself.
6.  is homeomorphic to
is homeomorphic to  . The homeomorphism is given by
. The homeomorphism is given by  . It follows that
. It follows that  is homeomorphic to a finite product with itself (product topology). Here we use the fact that if
is homeomorphic to a finite product with itself (product topology). Here we use the fact that if  is a continuous bijection with
is a continuous bijection with 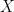 compact and
compact and  Hausdorff then
Hausdorff then 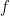 is a homeomorphism.
is a homeomorphism.
Now we can say a bit more: if 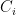 is a copy of
is a copy of  then
then  is homeomorphic to
is homeomorphic to  . This will follow from subsequent work, but we can prove this right now, provided we review some basic facts about countable products and counting.
. This will follow from subsequent work, but we can prove this right now, provided we review some basic facts about countable products and counting.
First lets show that there is a bijection between  and
and  . A bijection is suggested by this diagram:
. A bijection is suggested by this diagram:

which has the following formula (coming up with it is fun; it uses the fact that  :
:
 for
for 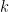 even
even
 for
for 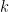 odd
odd
 for
for 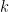 odd,
odd, 
 for
for 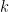 even,
even, 
Here is a different bijection; it is a fun exercise to come up with the relevant formulas:

Now lets give the map between  and
and  . Let
. Let  and denote the elements of
and denote the elements of  by
by  where
where  .
.
We now describe a map  by
by

Example: 
That this is a bijection between compact Hausdorff spaces is immediate. If we show that  is continuous, we will have shown that
is continuous, we will have shown that 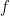 is a homeomorphism.
is a homeomorphism.
But that isn’t hard to do. Let  be open;
be open;  . Then there is some
. Then there is some  for which
for which  . Then if
. Then if  denotes the
denotes the  component of
component of 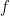 we wee that for all
we wee that for all  (these are entries on or below the diagonal containing
(these are entries on or below the diagonal containing  depending on whether
depending on whether  is even or odd.
is even or odd.
So  is of the form
is of the form  where each
where each  is open in
is open in  . This is an open set in the product topology of
. This is an open set in the product topology of  so this shows that
so this shows that  is continuous. Therefore
is continuous. Therefore  is a homeomorphism, therefore so is
is a homeomorphism, therefore so is  .
.
Ok, what does this have to do with Cantor Sets and Cantor Spaces?
If you know what the “middle thirds” Cantor Set is I urge you stop reading now and prove that that Cantor set is indeed homeomorphic to  as we have described it. I’ll give this quote from Willard, page 121 (Hardback edition), section 17.9 in Chapter 6:
as we have described it. I’ll give this quote from Willard, page 121 (Hardback edition), section 17.9 in Chapter 6:
The proof is left as an exercise. You should do it if you think you can’t, since it will teach you a lot about product spaces.
What I will do I’ll give a geometric description of a Cantor set and show that this description, which easily includes the “deleted interval” Cantor sets that are used in analysis courses, is homeomorphic to  .
.
Set up
I’ll call this set 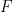 and describe it as follows:
and describe it as follows:
 (for those interested in the topology of manifolds this poses no restrictions since any manifold embeds in
(for those interested in the topology of manifolds this poses no restrictions since any manifold embeds in  for sufficiently high
for sufficiently high 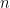 ).
).
Reminder: the diameter of a set  will be
will be 
Let  be a strictly decreasing sequence of positive real numbers such that
be a strictly decreasing sequence of positive real numbers such that  .
.
Let  be some closed n-ball in
be some closed n-ball in  (that is,
(that is,  is a subset homeomorphic to a closed n-ball; we will use that convention throughout)
is a subset homeomorphic to a closed n-ball; we will use that convention throughout)
Let  be two disjoint closed n-balls in the interior of
be two disjoint closed n-balls in the interior of  , each of which has diameter less than
, each of which has diameter less than 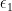 .
.

Let  be disjoint closed n-balls in the interior
be disjoint closed n-balls in the interior  and
and  be disjoint closed n-balls in the interior of
be disjoint closed n-balls in the interior of  , each of which (all 4 balls) have diameter less that
, each of which (all 4 balls) have diameter less that  . Let
. Let 

To describe the construction inductively we will use a bit of notation:  for all
for all  and
and  will represent an infinite sequence of such
will represent an infinite sequence of such  .
.
Now if  has been defined, we let
has been defined, we let  and
and  be disjoint closed n-balls of diameter less than
be disjoint closed n-balls of diameter less than  which lie in the interior of
which lie in the interior of  . Note that
. Note that  consists of
consists of  disjoint closed n-balls.
disjoint closed n-balls.
Now let  . Since these are compact sets with the finite intersection property (
. Since these are compact sets with the finite intersection property ( for all
for all 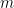 ),
), 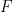 is non empty and compact. Now for any choice of sequence
is non empty and compact. Now for any choice of sequence  we have
we have  is nonempty by the finite intersection property. On the other hand, if
is nonempty by the finite intersection property. On the other hand, if  then
then  so choose
so choose  such that
such that  . Then
. Then  lie in different components of
lie in different components of  since the diameters of these components are less than
since the diameters of these components are less than  .
.
Then we can say that the  uniquely define the points of
uniquely define the points of 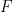 . We can call such points
. We can call such points 
Note: in the subspace topology, the  are open sets, as well as being closed.
are open sets, as well as being closed.
Finding a homeomorphism from 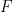 to
to  .
.
Let  be defined by
be defined by  . This is a bijection. To show continuity: consider the open set
. This is a bijection. To show continuity: consider the open set  . Under
. Under 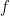 this pulls back to the open set (in the subspace topology)
this pulls back to the open set (in the subspace topology)  hence
hence 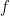 is continuous. Because
is continuous. Because 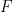 is compact and
is compact and  is Hausdorff,
is Hausdorff, 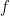 is a homeomorphism.
is a homeomorphism.
This ends part I.
We have shown that the Cantor sets defined geometrically and defined via “deleted intervals” are homeomorphic to  . What we have not shown is the following:
. What we have not shown is the following:
Let 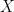 be a compact Hausdorff space which is dense in itself (every point is a limit point) and totally disconnected (components are one point sets). Then
be a compact Hausdorff space which is dense in itself (every point is a limit point) and totally disconnected (components are one point sets). Then 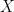 is homeomorphic to
is homeomorphic to  . That will be part II.
. That will be part II.
.
where
is, say, a manifold (a 2’nd countable metric space which has neighborhoods either locally homeomorphic to
or
. Note: though we often think of smooth or piecewise linear curves, we don’t have to do so. Also, we can allow for self-intersections.
; such a gadget is called a space filling curve.
cannot be one to one, because if it were, because the domain is compact,
would have to be a homeomorphism. But the respective spaces are not homeomorphic. For example: the closed interval is disconnected by the removal of any non-end point, whereas the closed square has no such separating point.
is a space filling curve, the inverse image of a points is actually an infinite number of points; the inverse (as a function) cannot be defined.


